Статья опубликована в рамках: LIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 23 декабря 2015 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИРОВАННОЙ СИСТЕМЫ ДЛЯ ВЫБОРА КАБЕЛЬНЫХ ЛИНИЙ ПРОМЫШЛЕННЫХ ПРЕДПРИЯТИЙ
Гладышева Мария Михайловна
доцент каф. вычислительной техники и программирования института энергетики и автоматизированных систем
ФГБОУ ВПО «МГТУ им. Г.И. Носова»,
РФ, г. Магнитогорск
E -mail: mar.ser.ksuh@gmail.com
Сухачева Евгения Константиновна
студент 2 курса института энергетики и автоматизированных систем
ФГБОУ ВПО «МГТУ им. Г.И. Носова»,
РФ, г. Магнитогорск
Хатюшина Татьяна Владимировна
студент 2 курса института энергетики и автоматизированных систем ФГБОУ ВПО «МГТУ им. Г. И. Носова»,
РФ, г. Магнитогорск
MATHEMATICAL MODEL OF AUTOMATED SOFTWARE SYSTEM FOR SELECTING A CABLE LINES INDUSTRIAL ENTERPRISES
Maria Gladisheva
candidate of Science, assistant professor of computer science and programming
Magnitogorsk State Technical University im. G.I. Nosov,
Russia, Magnitogorsk
Evgeniya Sukhacheva
2th year student of the Institute of Energy and automated systems,
Magnitogorsk State Technical University im. G.I. Nosov,
Russia, Magnitogorsk
Tatyana Hatyushina
2th year student of the Institute of Energy and automated systems,
Magnitogorsk State Technical University im. G.I. Nosov,
Russia, Magnitogorsk
аннотация
В статье рассматриваются основные характеристики кабельных линий и использование математической модели для правильного выбора кабельных линий промышленных предприятий.
ABSTRACT
The article examines the main characteristics of the cable lines and the use of mathematical models for the correct choice of cable lines of industrial enterprises.
Ключевые слова : кабельные линии; промышленные предприятия; программный продукт; программное обеспечение; электроснабжение; математическая модель.
Keywords : cable lines; industry; software; software; power supply; mathematical model.
Для повышения эффективности расчета характеристик кабельных линий и удобное хранения информации возникает вопрос о разработки программного обеспечения автоматизированной системы для выбора кабельных линий промышленных предприятий. В ходе анализа и сравнения существующего программного обеспечения для выбора кабельных линий промышленных предприятий [2] был выявлен ряд недостатков, в связи с чем разработка программного обеспечения является актуальной.
Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженное в математических терминах и сохраняющих существенные черты оригинала. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.
Математические модели для анализа режимов систем электроснабжения строятся, как правило, на основе функциональных моделей. Создание математической модели в этом случае обычно подразумевает составление схемы замещения исследуемой системы, определение ее параметров и расчет токов и напряжений известными математическими методами, используемыми в электротехнике при анализе электрических схем [1].
К основным характеристикам кабельной линии относятся: длинна кабельной линии; мощность нагрузки на кабель; напряжение сети; количество фаз; коэффициент мощности; допустимые потери напряжения; температура окружающей среды; способ прокладки кабеля; материал кабеля; нагрузка на кабель; коэффициент потерь; удельное сопротивление материала кабеля; сопротивление кабельной линии; плотность тока в кабеле; реальные потери напряжения; сечение токопроводящей жилы кабеля.
Для того чтобы выбрать правильную кабельную линию нужно рассчитать сечение токопроводящей жилы кабеля, а это возможно только если будут известны другие характеристики кабельной линии. В первую очередь нужно рассчитать нагрузку на кабель. Нагрузка на кабельную линию рассчитывается в зависимости от фазности сети:
1) для однофазной сети нагрузка рассчитывается по формуле 1:
|
|
(1) |
где: P – мощность нагрузки на кабель;
U – напряжение сети;
![]() – коэффициент одновременности;
– коэффициент одновременности;
cosφ – коэффициент мощности;
2) для трехфазной сети нагрузка рассчитывается по формуле 2:
|
|
(2) |
где: P – мощность нагрузки на кабель;
U – напряжение сети;
cosφ – коэффициент мощности.
На кабельной линии происходят потери напряжения и в зависимости от допустимых потерь напряжения рассчитывается коэффициент потерь по формуле 3:
|
|
(3) |
где ![]() – допустимая величина потерь по напряжению в линии, %.
– допустимая величина потерь по напряжению в линии, %.
Удельное сопротивление материала можно найти по таблице в справочниках по физике, но там значение удельного сопротивления представлены при температуре 20 ºС. На самом деле удельное сопротивление материала кабеля меняется в зависимости от температуры окружающей среды, и это изменение рассчитывается по формуле 4:
|
|
(4) |
где: ![]() – удельное сопротивление при температуре
– удельное сопротивление при температуре ![]() 20 ºС;
20 ºС;
![]() – температурный коэффициент удельного сопротивления при температуре
– температурный коэффициент удельного сопротивления при температуре ![]() 20 ºС;
20 ºС;
Т – температура окружающей среды.
Для выбора кабельной линии необходимо знать сечение токопроводящей жилы кабеля. Для расчета сечения воспользуемся формулой 5:
|
|
(5) |
где: ρ – удельное сопротивление жилы кабеля;
U – напряжение сети;
![]() – коэффициент потерь;
– коэффициент потерь;
L – общая протяженность кабельной линии;
P – мощность нагрузки на кабель.
Для расчета сопротивления кабельной линии воспользуемся формулой 6:
|
|
(6) |
где: ρ – удельное сопротивление жилы кабеля;
L – общая протяженность кабельной линии;
![]() – сечение токопроводящей жилы кабеля.
– сечение токопроводящей жилы кабеля.
Проверить выполненные расчеты можно путем определения реальных потерь напряжения в кабельной линии. Для этого воспользуемся формулой 7
|
|
(7) |
где: L – общая протяженность кабельной линии;
R – сопротивление кабельной линии.
Переведем полученное значение в проценты относительно напряжения полученного из сети по формуле 8
|
|
(8) |
где: ΔU – потери напряжения, В;
U – напряжение сети, В.
Для расчета плотности тока воспользуемся формулой 9
|
|
(9) |
где: ![]() – сечение токопроводящей жилы;
– сечение токопроводящей жилы;
I – нагрузка на кабель.
Таким образом, использование математической модели программного обеспечения автоматизированных систем в значительной мере упрощает выбор кабельных линий для промышленных предприятий.
Список литературы :
1. Веников В.А. Электрические системы. Математические модели электроэнергетики: учебник для студентов вузов / Под ред. В.А. Веникова – 2-е изд., перераб. И доп. – М.: Высш.шк., 1981. – 288 с.
2. Гладышева М.М., Сухачева Е.К., Хатюшина Т.В. Анализ и сравнение существующих программных продуктов при разработке программного обеспечения автоматизированной системы для выбора кабельных линий промышленных предприятий // Инновации в науке / Сб. ст. по материалам LI междунар. науч.-практ. конф. № 11 (48). Часть I. Новосибирск: Изд. АНС «СибАК», 2015. – C. 107–115.
3. Кондрашова Ю.Н., Газизова О.В., Гладышева М.М., Галлиулин И.М. Исследование влияния ввода в работу перспективной воздушной линии на режимы промышленного энергетического узла // Международный научно-исследовательский журнал. – 2014, – № 4-2(23). – С. 35–37.
дипломов


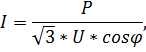
Оставить комментарий