К  ВОПРОСУ  О  РОЛИ  ПОЛИПЛОИДИИ  ПРИ  АНАЛИЗЕ  НАРУШЕНИЙ  МЕТАБОЛИЗМА,  ОБУСЛОВЛЕННЫХ  АКТИВИЗАЦИЕЙ  ТРАНСПОЗОНОВ

Бутов  Александр  Александрович

д-р  физ.-мат.  наук,  профессор,  заведующий  кафедрой  прикладной  математики 
Ульяновского  государственного  университета, 
РФ,  г.  Ульяновск

E -mail:  pm@ulsu.ru

Карев  Михаил  Андреевич

аспирант, 
Ульяновский  государственный  университет, 
РФ,  г.  Ульяновск

E -mail:  misha5490mk@yandex.ru

Коваленко  Анатолий  Александрович

студент  магистратуры, 
Ульяновский  государственный  университет, 
РФ,  г.  Ульяновск

E -mail:  anako09@mail.ru

Кононова  Галина  Викторовна

студент  магистратуры, 
Ульяновский  государственный  университет, 
РФя,  г.  Ульяновск

E-mail: 

ON  THE  QUESTION  ABOUT  A  CONTRIBUTION  A  POLYPLOIDY  ANALYZE  A  METABOLIC  IMBALANCE  ASSOCIATED  WITH  TRANSPOSONS  ACTIVATION

Alexander  Butov

doctor  of  Physical  and  Mathematical  Sciences,  professor,  head  of  the  department  of  Applied  Mathematics, 
Ulyanovsk  State  University, 
Russia,  Ulyanovsk

Mikhail  Karev

postgraduate  student, 
Ulyanovsk  State  University, 
Russia,  Ulyanovsk

Anatolyi  Kovalenko

master’s  student, 
Ulyanovsk  State  University, 
Russia,  Ulyanovsk

Galina  Kononova

master’s  student, 
Ulyanovsk  State  University, 
Russia,  Ulyanovsk

АННОТАЦИЯ

В  настоящей  работе  представлен  принцип  построения  модели  на  основе  телеграфных  процессов  в  семимартингальных  терминах  митоточески  активных  клеток,  учитывается  явление  полиплоидии,  эффект  активации  транспозонов.  Сформулирована  теорема.

ABSTRACT

This  article  presents  the  principle  of  formation  the  model  in  terms  of  telegraph  process  and  semimartingals  of  mitotic  activity  cells  considering  polyploidy,  transposons  activation.  A  theorem  was  formulated.

Ключевые   слова:  транспозон;  полиплоидия;  семимартингал.

Keywords:  transposon;  polyploidy;  semimartingal.

1.  Пусть  =  —  стохастический  базис  с  обычными  условиями  Деллашери  [1].  Пусть  при    заданы  точечные  процессы    и  ,  определяющие  позиции  активных  транспозонов  на  хромосомах  с  нормированными  длинами  (равными  1).  В  таких  обозначениях  наличие  активных  транспозонов  может  быть  обозначено  единичным  значением  процесса  телеграфного  типа

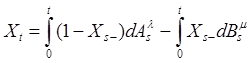  (1)

с  процессами    и  ,  имеющими  компенсаторы

,  ,    (2)

Обозначим  .  Тогда,  очевидно,  выполняется  соотношение

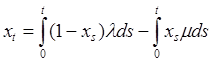        (3)

Обозначим  среднюю  длину  транспозона  .

Тогда,  очевидно

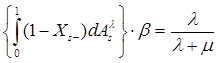       (4)

поскольку,  как  следует  из  уравнения  (3)

  (5)

(при  стационарном  распределении,  наблюдаемом  в  экспериментах    и,  следовательно,  выполняется  (5)).

Из  (4)  вытекает  полезное  соотношение  для  соотношения  частоты  затухания  активности  транспозонов  и  их  средней  длины

                   (6)

2. В  настоящей  работе  рассматривается  модель  митотически  активных  (т.  е.  не  постмитотических,  и  не  клеток  с  затухающей  митотической  активностью).  Для  таких  клеток  характерно  явление  полиплоидии.

Наряду  с  многими,  как  положительными,  так  и  отрицательными  эффектами  этого  явления,  наблюдается  некоторая  взаимосвязь  его  с  эффектами  активации  транспозонов.  Эта  взаимосвязь  проявляется  в  существовании  некоторых  компромиссных  уровней  (как  полиплоидии,  так  и  активации  транспозонов),  которые  позволяют  достигать  значений,  оптимальных  с  точки  зрения  угроз  канцерогенеза,  с  одной  стороны,  и  мутагенеза  активации  транспозонов,  с  другой  стороны.

Пусть  в  клетке  существует    (идентичных)  копий  хромосомы.  Тогда  локусы  активности  транспозонов,  разрушающие  работу  нормальной  ДНК  могут  быть  обозначены 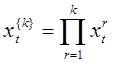 со  средними  значениями  на  всех  хромосомах  равными

  (7)

Последнее  равенство  следует,  очевидно  из  того,  что  ,  поскольку  при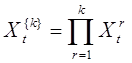 

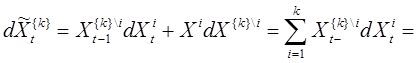
и,  следовательно

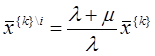
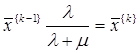
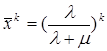         ,  (8)

что  приводит  к  нарушениям  экспрессии  генов  за  время  ,  пропорциональное  величине

  (9)

Таким  образом,  оптимизация  работы  генома  предполагает  за  некоторое  время    минимизацию

  (10)

Однако,  полиплоидия  (и  это  особенно  наглядно  демонстрирует  поведение  гепатоцитов)  приводит  к  росту  угрозы  канцерогенеза,  который  можно  в  первом  приближении  представить  в  виде  вероятности

  (11)

с  задачей 

  (12)

где    —  коэффициент  канцерогенной  активации  генов  на  любой  из    аллельных  хромосом  при  -полиплоидии.

Таким  образом  при  формировании  полиплоидных  структур  (наряду  с  иными  задачами  и  причинами  её  возникновения)  решается  задача  оптимизации,  аддитивно  формирующаяся  из  подзадач  (10)  и  (12):

,  (13)

где    —  некоторый,  экспериментально  (на  основе  эволюционного  обоснования  полиплоидии)  определяемый  коэффициент  пропорциональности.

Заметим,  что  количество  активных  транспозонов  существенно  ниже  их  общего  числа.  Это  приводит  к  соотношению  ,  а  также  к  тому,  что  ,  поскольку  общая  генетическая  масса  активных  транспозонов  существенно  меньше  общего  объема  хромосомы.

Следовательно,  задача  (13)  редуцируется  в  приближенную  задачу

  (14)

поскольку 

Теорема.  Решение  задачи  (14)  существует  и  определяется  трансцендентным  уравнением

,

где  .

Замечание.  Решение  не  только  существует,  положительно,  но  и  допускает  оценку  .

Список  литературы:

1.Бутов  А.А.  Теория  случайных  процессов  /  А.А.  Бутов,  К.О.  Раводин.  Ульяновск:  УлГУ,  2009.  —  62  с.

2.Карев  М.А.  Имитационная  стохастическая  модель  динамики  размножения  транспозонов  /  М.А.  Карев,  А.А.  Бутов  //  Естественные  и  технические  науки.  —  2013.  —  №  5(67).  —  С.  310—315.  —  ISSN  1684-2626.