Статья опубликована в рамках: XXIV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 05 ноября 2014 г.)
Наука: Физика
Секция: Кристаллография, физика кристаллов
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ПОЛЯ ДИРЕКТОРА НЕМАТИЧЕСКОГО ЖИДКОГО КРИСТАЛЛА В ЯЧЕЙКЕ С КОМПЛАНАРНЫМИ ЭЛЕКТРОДАМИ
Богатырев Борис Дмитриевич
магистр Южно-Уральского Государственного университета, РФ, г. Челябинск
E -mail: bogatyrevbd@yandex.ru
Клебанов Игорь Иосифович
доцент Челябинского государственного педагогического университета,os доцент Южно-Уральского Государственного университета, РФ, г. Челябинск
E-mail: klebanov.igor2010@yandex .ru
Подгорнов Федор Валерьевич
доцент Южно-Уральского Государственного университета, РФ, г. Челябинск
E -mail: fedorpod@yahoo.de
Иванов Сергей Александрович
старший преподаватель Челябинского государственного педагогического университета, старший преподаватель Южно-Уральского Государственного университета, РФ, г. Челябинск
E-mail: ivanovlord@ya .ru
MATHEMATICAL MODELLING OF SPATIAL DISTRIBUTION OF THE NEMATIC DIRECTOR FIELD IN THE CELL WITH IN-PLANE ELECTRODES
Bogatyrev Boris
undergraduate of the South-Ural State university, Russia, Chelyabinsk
Klebanov Igor
associate professor of Chelyabinsk State Pedagogical University, associate professor of South-Ural State University, Russia, Chelyabinsk
Podgornov Fedor
associate professor of South-Ural State University, Russia, Chelyabinsk
Ivanov Sergey
associate professor of Chelyabinsk State Pedagogical University, associate professor of South-Ural State University, Russia, Chelyabinsk
АННОТАЦИЯ
Рассматривается ячейка с компланарными электродами, заполненная нематическим жидким кристаллом. Получено точное аналитическое выражение для распределения электрического поля в ячейке. В одноконстантном приближении континуальной теории методом Ритца приближенно рассчитано распределение поля директора нематика в ячейке. Расчеты проведены для случаев планарных граничных условий и положительной диэлектрической анизотропии. Произведено сравнение теоретических результатов с экспериментальными. Установлено хорошее качественное соответствие теоретических и экспериментальных результатов.
ABSTRACT
The cell with in-plane electrodes filled with a nematic liquid crystal (NLC) is considered. Rigorous analytical expression for the spatial distribution of electric field across a cell is retrieved. In one-constant approximation of the continual theory the method of Rietz allows evaluating distribution of the director field of the NLC in a cell. Calculations are implemented for planar alignments of NLC and positive dielectric anisotropy. It was demonstrated that theoretical and experimental results are in good accordance.
Ключевые слова: жидкий кристалл; нематик; компланарные электроды; поле директора; математическая модель; метод Ритца.
Keywords: liquid crystal; nematic; in-plane electrodes; director field; mathematical model; Rietz method.
Жидкие кристаллы представляют собой мезофазное состояние между твердыми кристаллами и изотропной жидкостью, и имеют как свойства жидкой среды (вязкость), так и кристаллической (анизотропия свойств). Жидкие кристаллы проявляют свои уникальные свойства в узком диапазоне температур между кристаллической твердой и изотропной жидкойфазой.
При охлаждении изотропной жидкости образуется не кристаллическая фаза, а фаза нематика, в которой молекулы уже имеется ориентационная упорядоченность, но еще отсутствует позиционная. Молекулы все еще могут перемещаться по объему жидкого кристалла, а вязкость сдвига мало отличается от значения в жидкой фазе. Однако главная ось молекул ЖК имеет приоритетное макроскопическое положение. В данной работе рассматривается жидкий кристалл в фазе нематика.
Среднее макроскопическое направление осей молекул ![]() в виде единичного вектора называют директором ЖК. Поле директора ЖК и его изменение под действием внешних условий, в частности — границ ячейки и электрического поля, является основным вопросом при рассмотрении свойств жидкого кристалла.
в виде единичного вектора называют директором ЖК. Поле директора ЖК и его изменение под действием внешних условий, в частности — границ ячейки и электрического поля, является основным вопросом при рассмотрении свойств жидкого кристалла.
В ЖК возможна эластичная деформация трех типов (рис. 1): (a) splay — директор поворачивается в направлении радиальной оси ![]() , (b) twist — директор поворачивается в направлении азимутальной оси
, (b) twist — директор поворачивается в направлении азимутальной оси ![]() вдоль оси
вдоль оси ![]() , и (c) bend — директор также смещается в направлении азимутальной оси
, и (c) bend — директор также смещается в направлении азимутальной оси ![]() , но изменения происходят вдоль оси
, но изменения происходят вдоль оси ![]() [1].
[1].

Рисунок 1. Три возможных типа деформации директора ЖК: (a ) splay, (b) twist, (c) bend
Плотность энергии упругой деформации рассчитывается как
![]() (1)
(1)
Плотность электрической энергии равна
![]() (2)
(2)
Когда электрическое поле слабое, ![]() можно считать константой, независимой от значения напряженности поля. Первый член выражения не зависит от направления поля директора по отношению к полю, а потому при расчете им можно пренебречь.Таким образом, для расчетов можно упростить выражение для плотности энергии до
можно считать константой, независимой от значения напряженности поля. Первый член выражения не зависит от направления поля директора по отношению к полю, а потому при расчете им можно пренебречь.Таким образом, для расчетов можно упростить выражение для плотности энергии до
![]() (3)
(3)
Обе составляющие плотности свободной энергии зависят от взаимного расположения электрического поля и поля директора жидкого кристалла. При этом в равновесных условиях поле директора будет ориентировано так, чтобы минимизировать полную энергию жидкого кристалла, находящегося в ячейке.
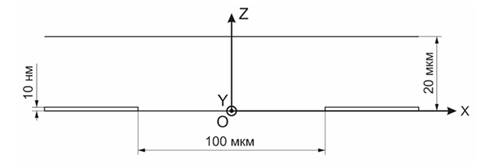
Рисунок 2. Чертеж ячейки с компланарными электродами в плоскости OXZ
Следовательно, функция распределения поля директора ![]() будет такова, чтобы интеграл плотности свободной энергии ЖК был минимален. Исходя из этого, можно найти распределение поля директора.
будет такова, чтобы интеграл плотности свободной энергии ЖК был минимален. Исходя из этого, можно найти распределение поля директора.
В рамках данной работы рассматривается ячейка с компланарными электродами (рис. 2). Электроды в такой ячейке располагаются в одной плоскости, напыленные на подложку в виде двух параллельных прямоугольников с фиксированным расстоянием между краями электродов.Для расчетов взята ячейка со следующими параметрами: толщина ячейки ![]() , расстояние между электродами
, расстояние между электродами ![]() , толщина напыленных электродов
, толщина напыленных электродов ![]() не более 10 нм, что позволяет нам пренебречь ими при расчете и считать идеально плоскими [2; 3].
не более 10 нм, что позволяет нам пренебречь ими при расчете и считать идеально плоскими [2; 3].
Расчет электрического поля в ячейке проводится на основе решения задачи Дирихле для полуплоскости. Так как нам известно распределение потенциала на границе полуплоскости (![]() ), а в остальном объеме оно удовлетворяет уравнению Лапласа
), а в остальном объеме оно удовлетворяет уравнению Лапласа ![]() , мы можем воспользоваться известным решением:
, мы можем воспользоваться известным решением:
![]() (4)
(4)
где
 (5)
(5)
![]()
 (6)
(6)
Составляющие вектора электрического поля есть производные от потенциала по соответствующим координатам:
 (7)
(7)
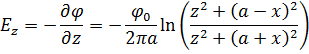 (8)
(8)
Плотность энергии в жидком кристалле складывается из двух составляющих — упругой и электрической. С учетом одноконстантного приближения (![]() ), представления вектора
), представления вектора ![]() в виде
в виде ![]() и того, что в жидком кристалле отсутствуют деформации типа twist, выражение для плотности энергии принимает следующий вид:
и того, что в жидком кристалле отсутствуют деформации типа twist, выражение для плотности энергии принимает следующий вид:
![]() (9)
(9)
Тогда общая энергия жидкого кристалла в ячейке
 (10)
(10)
Минимизации полной энергии ячейки приводит к уравнению Эйлера-Лагранжа для равновесного распределения поля директора.Но, так как компоненты электрического поля являются сложными функциями координат,данное уравнение не решается аналитически. Численный расчет также является сложной задачей в силу нелинейности уравнения равновесия.
Поэтому в настоящей работе найдено приближенное выражение для распределения поля директора методом Ритца.
|
Предварительно сделаем подстановку:
![]()
Тогда выражение для плотности энергии примет следующий вид:
![]() (11)
(11)
Примем нулевые граничные условия:
![]() (12)
(12)
И будем искать приближенное решение в виде
![]() (13)
(13)
Функция ![]() выбирается так, чтобы удовлетворять тем же граничным условиям:
выбирается так, чтобы удовлетворять тем же граничным условиям:
![]()
После подстановки (11) и (13) в (10) получим функцию, зависящую только от коэффициентов ![]() и
и ![]() . При низких значениях прикладываемого потенциаладанная функция имеет один локальный минимум в начале координат (
. При низких значениях прикладываемого потенциаладанная функция имеет один локальный минимум в начале координат (![]() ), что соответствует неискаженной картине поля с
), что соответствует неискаженной картине поля с ![]() . Однако при увеличении напряжения выше 7,5 В картина начинает меняться — в начале координат наблюдается появление максимума, а симметрично относительно него возникают два глобальных минимума(
. Однако при увеличении напряжения выше 7,5 В картина начинает меняться — в начале координат наблюдается появление максимума, а симметрично относительно него возникают два глобальных минимума(![]() ), соответствующие новому устойчивому состоянию жидкого кристалла. Это соответствует известному в физике жидких кристаллов эффекту перехода Фредерикса.
), соответствующие новому устойчивому состоянию жидкого кристалла. Это соответствует известному в физике жидких кристаллов эффекту перехода Фредерикса.
Так как функция F(C1,С2) в явном виде сложна для аналитического исследования, зависимость от коэффициентов полинома получена численно для каждого значения напряжения в отдельности. Затем, с помощью метода наискорейшего спуска были найдены координаты одного из двух глобальных минимумов. Координаты представлены в таблице ниже:
Таблица 1.
|
Напряжение, В |
|
|
|
7,5 |
1,2 |
16,7 |
|
10 |
11,85 |
99,1 |
|
20 |
36,8 |
-302,1 |
|
30 |
56,1 |
-789,5 |
Подставим найденные полиномиальные коэффициенты в уравнение и проведем обратную замену, чтобы получить распределение поля директора.
Полученные в рамках моделирования результаты (рис. 3) качественно совпадают с экспериментальными результатами, полученными при изучении ячеек с компланарными электродами. Проверка соответствия теоретического распределения поля директора проводится на основе оценки диэлектрофоретической силы, действующей на микрочастицу диаметром 2 мкм вблизи от края электрода на расстоянии 15 мкм от плоскости электродов.
![]() (15)
(15)
что совпадает по порядку с приведенными в статье [2] величинами.
Полученное напряжение перехода ЖК из неискаженного состояния в искаженное соответствует напряжению перехода Фредерикса, полученному экспериментально для сходных условий (![]() ) [3].
) [3].
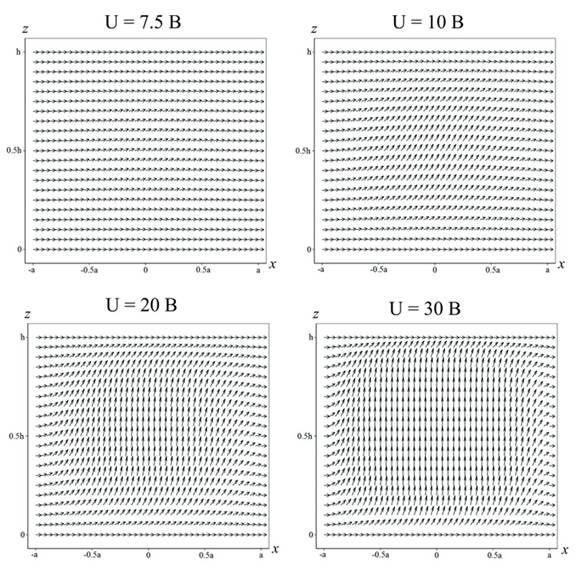
Рисунок 3. Результаты расчета пространственного распределения поля директора в зависимости от напряжения на электродах
Однако данная теоретическая модель может быть применима только в диапазоне напряжений до 30 В. При превышении данной разности потенциалов на электродах теоретическая зависимость искажается и приводит к результатам, противоречащим экспериментальным данным. Скорее всего, причина этого — малое количество слагаемых в (13). Увеличение количества слагаемых требует разработки более сложной программы поиска глобальных минимумов энергии нематика, что является предметом дальнейшей работы.
Список литературы:
1.Yang, Deng-Ke. Fundamentals of Liquid Crystal Devices / Deng-Ke Yang, Shin-Tson Wu – John Wiley & Sons Ltd, 2006 — 397 с.
2.Measurements of the electrokinetic forces on dielectric microparticles in nematic liquid crystals using optical trapping / А.В. Рыжкова, Ф.В. Подгорнов, A. Gaebler, R. Jakoby, W. Haase // J. Appl. Phys. 113, 244902 (2013).
3.Nonlinear electrophoretic motion of dielectric microparticles in nematic liquid crystals / А.В. Рыжкова, Ф.В. Подгорнов, W. Haase // Applied Physics Letters 96, 151901 (2010).
дипломов


Оставить комментарий