Статья опубликована в рамках: XVI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 28 января 2013 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
ОПЫТНАЯ ПРОВЕРКА ВЕРОЯТНОСТНОЙ МОДЕЛИ ИЗМЕЛЬЧЕНИЯ С ИСПОЛЬЗОВАНИЕМ КВАРЦЕВОЙ РУДЫ
Каримова Люция Монировна
канд. хим. наук, вед. науч. сотр. «НИЦИТ» ТОО «КазГидроМедь», г. Караганда
Кайралапов Ерлан Токпаевич
инженер-исследователь «НИЦИТ» ТОО «КазГидроМедь», г. Караганда
E-mail:
EXPERIMENTAL VERIFICATION OF PROBABILISTIC MODELSGRINDING WITH QUARTZ ORE
Lutsia Karimova
c.c.s, Leading research worker
"RCIT” LLP"KazGidroMed" Karaganda
Yerlan Kayralapov
Research Engineer "RCIT "
LLP "KazGidroMed" Karaganda
АННОТАЦИЯ
Проведена проверка теоретической модели измельчения по данным переработки монофракции кварцевой руды в лабораторной шаровой мельнице при водопадном режиме работы.
ABSTRACT
Audited theoretical model of grinding according monofraktsii quartz ore processing in the laboratory ball mill at a waterfall mode.
Ключевые слова: шаровая мельница; константа скорости измельчения; кварцевая руда;
Key words: ball mill; grinding rate constant; quartz ore;
В работах по обоснованию вероятностной модели измельчения найдено [1—4] наиболее общее выражение скорости процесса через частотный (Z), стерический (Рст), активационный (Ра) и концентрационный (Рконц.) факторы:
![]() (1)
(1)
Адаптация этих факторов к условиям работы мельниц была выражена соответственно как
![]() , (2)
, (2)
![]() , (3)
, (3)
 , (4)
, (4)
 (5)
(5)
где: ω — частота вращения мельницы, с-1;
D — внутренний диаметр мельницы, м;
g — ускорение силы тяжести, м/с2;
dj — средний размер зерен фракции с индексом j в порядке уменьшения размера, м;
dш — диаметр мелющего шара, м;
Еа — энергия активации измельчения, Дж/моль;
М — молекулярная масса самой твердой составляющей зерна (обычно, кварца), кг/моль;
m — масса мелющего шара, кг;
γз — плотность руды (зернового материала), кг/м3;
R— универсальная газовая постоянная, Дж/(моль·К);
Т — абсолютная температура (обычно принимаемая равной 298 К);
Gз — масса руды в мельнице (зерен), кг;
Gш — масса шаров в мельнице, кг;
γш — плотность шаров, кг/м3;
Gви γв — масса и плотность воды в мельнице, кг и кг/м3;
Рj — долевое содержание фракции со средним размером зерна dj.
В результате уравнение для скорости процесса измельчения имеет вид с учетом функционального изменения только долевого содержания фракции Рj
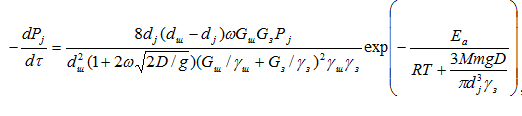 , (6)
, (6)
в котором в константу скорости измельчения для каждой фракции входят все постоянные параметры, кроме Рj
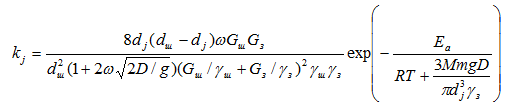 . (7)
. (7)
В свою очередь, эта константа вводится в интегральную модель измельчения, учитывающую не только убыль содержания каждой фракции, но и прирост его (кроме первого) за счет образования осколков от предыдущей фракции в строгом соответствии с кинетикой последовательных химических и физических превращений [1—4]:
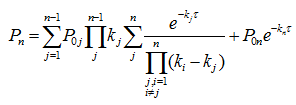 , (8)
, (8)
где: n — номер рассчитываемой фракции,
j — номера предыдущих фракций и соответствующих стадий разрушения зерен,
P0j — исходное долевое содержание фракций,
τ — продолжительность измельчения, с.
Опыты проводили в лабораторной шаровой мельнице 62 МЛ на жильном кварце месторождения Актас (Карагандинская область), содержащем (%): SiO2 — 99,8; Al2O3 — 0,15; Fe2O3 — 0,03; CaO — 0,006; TiO2 — 0,004. Для проверки принципиальной применимости вероятностной модели (8) использовали монофракцию –1+0,5 мм со средним диаметром 7,5·10-4 м общей массой Gз=0,200 кг, плотностью γз=2650 кг/м3.Стальные шары размером dш=0,0221 м, массой m=0,0476 кг, плотностью γш=7874 кг/м3 и общей массой Gш=1,470 кг загружали в мельницу вместе с водой массой Gв=0,350 кг и плотностью γв=1000 кг/м3. Внутренний диаметр мельницы составил D=0,1455 м, угловая скорость вращения ωдля поддержания водопадного режима задавалась равной 1,87 с-1.
Молекулярная масса кварца М=0,0601 кг/моль, в качестве энергетического барьера активации в соответствии с рекомендациями авторов [1—4] и на основе представлений о разрушении кристаллов, инициируемом пластической деформацией [5], задавали равном теплоте плавления кварца Еа=9170 Дж/моль.
При фракционном анализе продуктов измельчения использовали набор сит, начиная с первой фракции –1+0,5 мм (d1=7,5·10-4 м), далее вторая –0,5+0,2 мм (d2=3,5·10-4 м), третья –0,2+0,1 мм (d3=1,5·10-4 м) и суммарно нижняя фракции –0,1 мм. В отношении представления последней фракции средним размером для сопоставления с результатами расчета по модели (8) существуют определенные проблемы, так как по новой модели тонкие классы учитываются более детально в полном соответствии с действительным фракционным составом нижнего класса, измельчение которого подчинено общим закономерностям последовательного разрушения зерен примерно на 8 осколков, т. е. с уменьшением размера в среднем в два раза, вплоть до сколь угодно малого размера [5]
![]() . (9)
. (9)
Поэтому для сопоставления с выходом нижней фракции следует просуммировать расчетные значения всех тонких классов, начиная с Рj+1, где jотносится к среднему размеру предпоследней ситовой фракции, в данном случае к d4=8,55·10-5 м.Результаты расчета представлены в таблице 1 и на рисунке 1.
Таблица 1.
Зависимость опытного и расчетного выхода фракций (Pэ и Pр) от продолжительности (τ) измельчения монофракциикварцевой руды –1+0,5 мм
j |
dj,м |
kj, c-1 |
τ=0 |
τ=900 с |
τ=1320 с |
τ=1800 с |
||||
Рэ |
Рр |
Pэ |
Pр |
Pэ |
Pр |
Pэ |
Pр |
|||
1 |
7,500·10-4 |
2,395·10-3 |
1 |
1 |
0 |
0,116 |
0 |
0,042 |
0 |
0,013 |
2 |
3,500·10-4 |
4,158·10-3 |
0 |
0 |
0,090 |
0,125 |
0,020 |
0,052 |
0 |
0,018 |
3 |
1,500·10-4 |
2,262·10-3 |
0 |
0 |
0,400 |
0,307 |
0,255 |
0,207 |
0,125 |
0,105 |
4 |
8,550·10-5 |
1,315·10-3 |
- |
0 |
- |
0,304 |
- |
0,361 |
- |
0,310 |
5 |
4,275·10-5 |
6,612·10-4 |
- |
0 |
- |
0,127 |
- |
0,262 |
- |
0,375 |
6 |
2,138·10-5 |
3,311·10-4 |
- |
0 |
- |
0,020 |
- |
0,068 |
- |
0,154 |
7 |
1,069·10-5 |
1,656·10-4 |
- |
0 |
- |
0,001 |
- |
0,007 |
- |
0,023 |
8 |
5,344·10-56 |
8,283·10-5 |
- |
0 |
- |
0 |
- |
0 |
- |
0,001 |
9 |
2,872·10-6 |
4,142·10-5 |
- |
0 |
- |
0 |
- |
0 |
- |
0 |
|
-0,1 мм |
0 |
0 |
0,510 |
0,452 |
0,725 |
0,698 |
0,875 |
0,863 |
|
|
Σ |
1 |
1 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
В целом сравниваемые массивы экспериментальных и расчетных данных без какого-либо систематического завышения или занижения достаточно адекватно отображают друг друга, о чем свидетельствует высокий коэффициент нелинейной множественной корреляции R=0,987 с его значимостью tR=1440>2, которым гарантируется статистическая надежность математической модели измельчения с 95 % уровнем достоверности. При этом высокая степень детерминации модели D=R2=0,974 подтверждает ее функциональность при всей вероятностной природе самого процесса измельчения и его отображения проверяемой моделью.
Таким образом, проведенная проверка теоретической модели измельчения по данным переработки монофракции кварцевой руды в лабораторной шаровой мельнице при водопадном режиме работы свидетельствует о строгости использованной модели измельчения, сопоставимой с корректностью закономерностей химической кинетики.

Крестики — экспериментальные данные, линии — по уравнению (8) для фракции –1+0,5 мм (1); –0,5+0,2 мм (2); –0,2+0,1 мм (3); –0,1 мм (4)
Рисунок 1. Зависимость выхода фракций кварцевой руды от продолжительности измельчения монофракции –1+0,5 мм
Список литературы:
1. Малышев В.П. Разработка теории соударений для измельчения материалов // Компл. использ. минер. сырья. — 1992. — № 12. — С. 43—49.
2. Малышев В.П. Новый аспект в теории измельчения руд и управления этим процессом // Обогащение руд. — 1995. — № 4—5 (240—241). — С. 4—14.
3. Малышев В.П., Турдукожаева А.М., Кайкенов Д. Развитие теории измельчения руд на основе молекулярных подходов. // Обогащение руд. — 2012. — № 4. — С. 29-35.
4. Малышев В.П. Самоорганизация процесса измельчения руд в шаровых мельницах как результат подобия с кинетикой последовательных химических реакций. // Автоматика-информатика. — 2012. — № 3—4. — С. 15—31.
5. Ходаков Г.С. Физика измельчения. — М.: Наука, 1972. — 308 с.
дипломов


Оставить комментарий