Статья опубликована в рамках: XLI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 28 января 2015 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
АЛГОРИТМ МОДЕЛИРОВАНИЯ ВЫХОДНОГО НАПРЯЖЕНИЯ НЕПОСРЕДСТВЕННОГО ПРЕОБРАЗОВАТЕЛЯ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
Прошин Иван Александрович
д-р техн. наук, зав. кафедрой «Автоматизация и управление», профессор Пензенского государственного технологического университета, РФ, г. Пенза
E -mail: proshin.Ivan@inbox.ru
Салмов Евгений Николаевич
аспирант кафедры «Автоматизация и управление», Пензенского государственного технологического университета, РФ, г. Пенза
THE ALGORITHM FOR MODELING OF OUTPUT VOLTAGE OF DIRECT ELECTRICAL ENERGY CONVERTER
Ivan Proshin
d octor of Technical Sciences, Head of "Automation and Control" department, professor of Penza State Technological University, Russia, Penza
Evgeniy Salmov
graduate student of "Automation and Control" department, Penza State Technological University, Russia, Penza
АННОТАЦИЯ
Работа направлена на разработку алгоритма формирования выходного напряжения непосредственного преобразователя электрической энергии на основе описания, включающего вектор синусоидального напряжения с дискретно управляемой начальной фазой и диагональную переключающую матрицу.
ABSTRACT
The work is aimed at developing an algorithm generating the output voltage of direct electrical energy converter based on a description that includes sinusoidal voltage vector with discrete controlled initial phase and diagonal switching matrix.
Ключевые слова: алгоритм; непосредственный преобразователь электрической энергии; моделирование.
Keywords: algorithm; direct electrical energy converter; modeling.
Математическое моделирование непосредственных преобразователей электрической энергии (НПЭ), широко используемых в промышленности, на основе существующих подходов с моделированием каждого переключающего элемента (ПЭ) сопряжено с необходимостью задания множества возможных состояний каждого из ПЭ [1—8]. Такой метод моделирования достаточно трудоёмок, требует при изменении режимов управления изменения алгоритмов переключения, что значительно усложняет исследование вентильно-электромеханических систем с НПЭ.
Действительно, число возможных состояний НПЭ при непрерывном режиме работы определяется выражением:
|
|
(1) |
где: m — число входных фаз;
n — число выходных фаз;
k — минимально возможное число фаз выходного напряжения.
Таким образом, для НПЭ с n = 3 и m = 6 количество используемых состояний при непрерывном режиме работы равно:

В работе рассмотрен алгоритм моделирования выходного напряжения НПЭ на основе предложенного авторами метода [1—3]. Выходное напряжение НПЭ в соответствии с разработанным методом математического моделирования представляется в виде единственного гармонического колебания с дискретно управляемой начальной фазой.
В каждый момент времени к выходу НПЭ с раздельным управлением подключается только одна ЭДС из множества ЭДС, поступающих на вход.
На вход НПЭ подаётся m-фазная система входных напряжений
Ui (ωВХt) = Um sin(ωВХt – φi), ![]() (2)
(2)
где: Ui(ωВХt) — мгновенное значение входного напряжения;
Um — амплитудное значение входного напряжения;
ωВХ — круговая частота;
φi — фазовый сдвиг.
На выходе НПЭ формируется напряжение с количеством фаз n, мгновенным значением напряжения Ui(ωВЫХt), амплитудным значением напряжения Um2, фазовым сдвигом φi и круговой частотой ωВЫХ.
Гармоническое колебание с дискретно управляемой начальной фазой задаётся следующим выражением:
|
|
(3) |
Процедура непосредственного преобразования электрической энергии n‑фазного НПЭ с раздельным управлением задаётся системой уравнений:
|
|
(4) |
Предлагается все возможные способы управления НПЭ задать переключающими функциями:
|
|
(5) |
где: l = 2·kf·π/Δϕ -1 = kf·m – 1;
kf = ωВХ/ωВЫХ — коэффициент преобразования частоты;
Ni — коэффициент, определяемый соотношением амплитуд различных полуволн выходного напряжения;
ni — коэффициент, определяющий фазовое положение полуволны входного напряжения в выходном напряжении.
На рисунках 1—3 показан алгоритм формирования кривых выходного напряжения НПЭ.
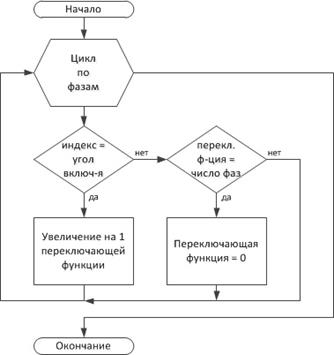
Рисунок 1. Закон изменения переключающих функций начальной фазы
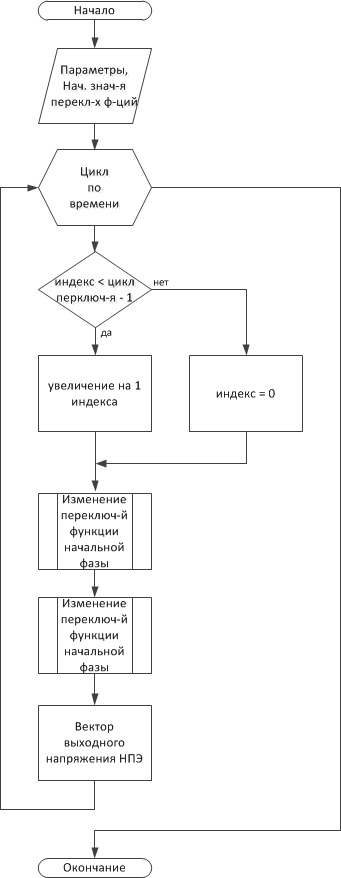
Рисунок 2. Основной цикл
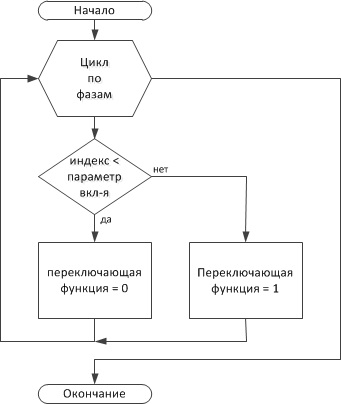
Рисунок 3. Закон изменения переключающих функций амплитуды
На рисунках 4—5 представлены результаты моделирования НПЭ на основе математической модели (4) и представленного алгоритма в среде Mathcad.
Для системы приняты значения: число фаз входного напряжения m = 9, входная частота f = 60 Гц, фазовый угол включения тиристоров α = 0 эл. град. На рисунках обозначено: XA — выходное напряжение в фазе А, YA — выходной ток в фазе А.
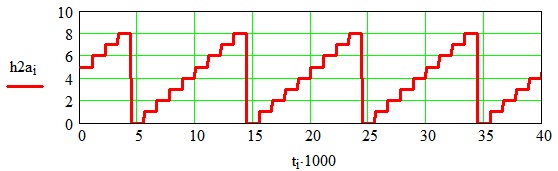
Рисунок 4. Изменение переключающей функции начальной фазы
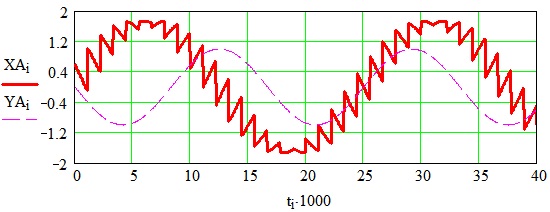
Рисунок 5. Выходное напряжение и ток НПЭ в фазе А (ток опережает напряжение на 90 эл.град.)
Предложен алгоритм формирования выходного напряжения НПЭ на основе описания, отличающегося от известных, наличием вектора синусоидального напряжения с дискретно управляемой начальной фазой и диагональной переключающей матрицы. Проведено математическое моделирование НПЭ. На базе алгоритма и метода математического моделирования возможно исследование многодвигательных многосвязных вентильно-электромеханических систем с НПЭ.
Список литературы:
1.Прошин И.А. Управление в вентильно-электромеханических системах. Кн. 1. Управление непосредственным преобразованием электрической энергии. Пенза: ПТИ, 2003. — 333 с.
2.Прошин И.А, Прошин А.И., Мещеряков А.С. Математическая модель асинхронного двигателя с непосредственным преобразователем энергии в цепях статора // Наука производству, — 1998, — № 4. — С. 13—15.
3.Прошин И.А. Теоретические основы моделирования управляемых вентильно-электромеханических систем с непосредственными преобразователями электрической энергии // Информационные технологии в проектировании и производстве, — 2000, — № 4. — С. 65—70.
4.Прошин И.А., Прошин А.И., Обухов В.А., Мещеряков А.С. Математическая модель валогенераторной установки // Наука производству, — 1998, — № 12. — С. 56—58.
5.Прошин И.А., Прошин А.И., Мещеряков А.С. Математическая модель электродинамического вибростенда // Наука производству, — 1998, — № 12. — С. 59—61.
6.Прошин И.А., Мещеряков А.С. Двухдвигательный электропривод роликоопор // Техника машиностроения, — 1996, — № 2. — С. 63—64.
7.Прошин И.А., Сапунов Е.А. Моделирование привода динамического стенда авиационного тренажера // Известия Самарского научного центра Российской академии наук. — 2011. — Т. 13 — № 1(2). — С. 337—340.
8.Proshin I.A., Salmov E.N. Mathematical modeling of the direct electrical energy converter. European Conference on Innovations in Technical and Natural Sciences. The 2nd International scientific conference proceedings (Маy 12, 2014). Vienna: OR: «East West» Association for Advanced Studies and Higher Education GmbH, 2014 — P. 47—52.
дипломов


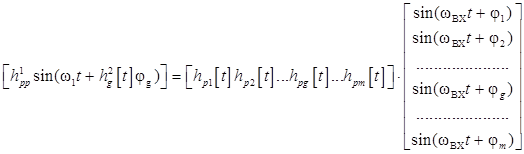
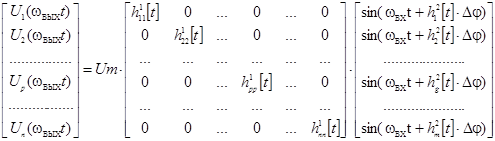
Оставить комментарий