КОМПЬЮТЕРНАЯ ОБУЧАЮЩАЯ СИСТЕМА «АЛГЕБРА ЛОГИКИ»

Ультан Александр Ефимович

канд. техн. наук, Сибирская Автомобильно-Дорожная Академия, г. Омск

E-mail: ultan_ae@mail.ru

Кравцов Дмитрий Александрович

аспирант, Сибирская Автомобильно-Дорожная Академия, г. Омск

E-mail: dkjazz@rambler.ru

Создание и совершенствование компьютеров привело и продолжает приводить к созданию новых технологий в различных сферах научной и практической деятельности. Одной из таких сфер стало образование – процесс передачи систематизированных знаний, навыков и умений от одного поколения к другому. Будучи само по себе мощной информационной сферой, и владея опытом использования различных классических (не компьютерных) информационных систем, образование быстро откликнулось на возможности современной техники. На наших глазах возникают нетрадиционные информационные системы, связанные с обучением [1].

Рисунок 1 – Комплекс обучающих программ «Учитель»

Разрабатываемый нами обучающий информационный комплекс «Учитель» является многомодульным. Пользователь имеет возможность подгружать различные модули, обучающие химии, алгебре, геометрии, физике и т. д. и единообразно работать с ними (рисунок 1). В данной статье описываются возможности модуля «Алгебра логики».

Работая с этим модулем, пользователь может, прежде всего, ввести и отредактировать любое логическое высказывание, содержащее операции дизъюнкция, конъюнкция, импликация, эквивалентность, отрицание, а так же выражение в скобках и систему логических выражений. Данный модуль уже на сегодняшний день обладает интеллектуальными функциями автоматического решения и обучения пользователя.

Программа позволяет вычислять истинность введенного логического высказывания при заданной истинности его аргументов (рисунок 2).

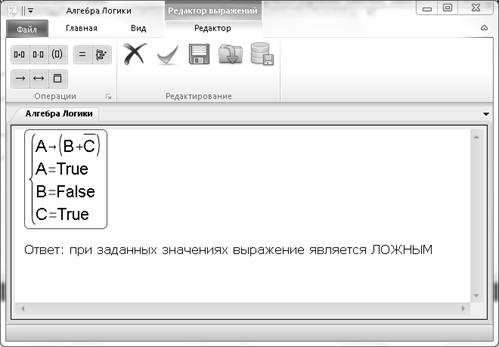
Рисунок 2 – Нахождение истинности логического высказывания

Возможно более подробное определение истинности логического высказывания с помощью вычисления таблицы истинности (рисунок 3). Таблица истинности, как известно, позволяет также доказывать тождественность логических выражений и решать текстовые задачи по алгебре логики. Для этого разработан соответствующий интерфейс, позволяющий пользователю открыть нужную текстовую задачу, увидеть ее текст на экране, формализовать данный текст в виде соответствующего логического высказывания (рисунок 4) и решить полученную задачу (рисунок 5).

В режиме  «автоматическое решение» программа способна решать самостоятельно от начала и до конца предоставленную задачу с выводом на экран пошагового решения, включая комментарии к произведенным действиям.

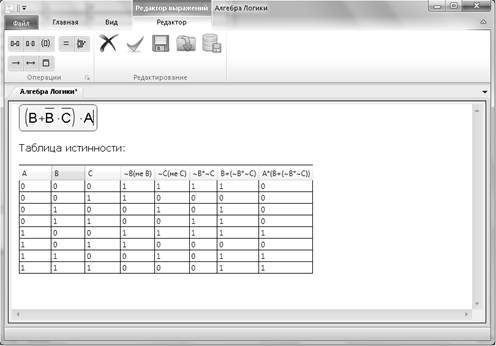
Рисунок 3 – Построение таблицы истинности

В режиме «контроль за ходом пользовательского решения» программа способна контролировать пошаговое решение пользователя, и предоставляет следующие функции: обнаружение ошибок, выдача по запросу пользователя подсказок о выявленных возможных действиях в текущем состоянии, осуществление шага решения по требованию пользователя, автоматическое решение до конца по требованию пользователя.

Рисунок 4 – Формализация текстовой задачи

Рисунок 5 – Решение задачи

Важно отметить, что в модуле «Алгебра логики» используется тот же WPF-компонент «Высказывание», что и в модуле «Алгебра». Этот компонент использует древовидную структуру или дерево для компьютерного моделирования математического выражения. Он отражает синтаксическую структуру математического выражения и хорошо подходит для дальнейшей обработки [2]. На рисунке 6 показан пример представления выражения в виде дерева.

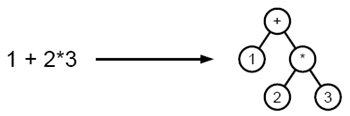
Рисунок 6 - Пример представления выражения в виде дерева

Компонент «Высказывание» представляет любое высказывание в виде дерева объектов, где узлами являются элементы-операции этого высказывания, а листовые объекты – это операнды. В этом плане все высказывания аналогичны. Отличие в том каковы узлы и листовые объекты для алгебры и для алгебры логики. Подобное представление высказывания позволяет делать прямой или обратный обход, анализировать поддеревья, выполнять различные преобразования и вычисления. Компонент «Высказывание» реализует множество функций для работы с данной структурой:

·     построение и редактирование дерева выражений (при этом, дерево-выражение может обладать разной внешностью. Например, логическое выражение может обладать как традиционной внешностью, так и внешностью-картинкой изображающей некоторую контактную схему или логическую схему);

·обход и поиск элементов дерева, используя различные алгоритмы;

·вычисление выражения, с использованием различных «вычислителей»;

·проведение тождественных преобразований с опорой на тождества соответствующие данному типу выражения;

·сохранение в файл и загрузка из файла;

·печать.

Дерево выражений компонента «Высказывание» имеет гибкую возможность расширения. Кроме того компонент «Высказывание» решает проблему отображения математической записи в нужном для пользователя виде. При этом логика отображения полностью отделяется от самого дерева выражений, что позволяет легко разрабатывать различные представления математических выражений, а также организовывать различные вычислительные процессы, не зависимо от представления высказывания на экране. Например, математическое выражение может быть представлено в интерфейсе программы как «иерархическое» или как запись в инфиксной нотации. Кроме того для тех, кто только начинает знакомство с математикой вместо цифр могут быть использованы и другие объекты для счета (например, палочки).

Разрабатываемая нами обучающая система по алгебре логике позволит пользователю самостоятельно и эффективно заниматься предметом. С одной стороны система способна автоматически решить ту или иную задачу, с другой стороны – контролировать процесс решения пользователя, указывая на ошибки и предоставляя качественные объяснения.

Список литературы:

1.Гагарина Л.Г. Алгоритмы и структуры данных. Гагарина Л.Г., Колдаев В.Д.  – М: Финансы и статистика, - 2009 – 303 с.

2.Роберт И.В. Основные направления научных исследований в области информатизации профессионального образования // И.В. Роберт, В.А. Поляков. – М.: Образование и Информатика, 2004.