ИССЛЕДОВАНИЕ МАТРИЧНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ РИККАТИ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Копец Мирослав Михайлович

канд. физ.-мат. наук, доцент НТУУ «КПИ», г. Киев

Е-mail: miroslav1941@windowslive.com

1.    Введение

Диффенциальное уравнение Риккати — это диффенциальное уравнение первого порядка, правая часть которого представляет собой квадратный трехчлен относительно неизвестной функции. Таким названием это уравнение обязано статье итальянского математика Якопо Франческо Риккати, опубликованной в 1724 году [14]. Несмотря на прошедшие почти три столетия, интерес к уравнению Риккати нисколько не ослабевает. В первую очередь к уравнениям Риккати приводят задачи оптимального управления, задачи теории дифференциальных игр, задачи построения оптимальных фильтров Калмана — Бьюси, двухточечные краевые задачи с использованием метода прогонки. Также уравнения Риккати появляются при решении задач динамики процессов в сплошных средах, задач теории теплопроводности и диффузии, задачи нахождения решений матричных телеграфных уравнений. В основном, в перечисленных выше случаях, как правило, приходится исследовать матричные диффенциальные урав­нения Риккати, в которых неизвестная зависит только от одной перемен­ной. Такая ситуация возникает тогда, когда рассматриваются системы со сосредоточенными параметрами. Именно для таких случаев основные свойства матричных диффенциальных уравнений Риккати изучены наиболее полно [1]—[6], [10]—[13]. Для математических моделей систем с распределенными параметрами возникают матричные диффен­циальные уравнения Риккати с частными производными [7], [9], [12] ,матричные интегродиффенциальные уравнения Риккати, которые менее исследованы по сравнению с обычными матричными диффенциаль­ными уравнениями Риккати.

 2. Постановка задачи

Рассматривается следующая система уравнений

 (1)

где , , — заданные матрицы размера ,  — заданная матрица размера , — заданная симметричная положительно определенная матрица размера ( поэтому существует матрица ), причем все эти пять матриц — постоянные (их элементами являются действительные числа),  — симметричная неотрицательно определенная матрица размера , символы ,  и  соответственно обозначают транспонированные матрицы , и . Заданы действительные числа  и такие, что  , . Искомая матричнозначная функция  при каждой упорядоченной паре  фиксированных значений  и имеет размер  и удовлетворяет условию

,                                                        (2)

где: — симметричная неотрицательно определенная матрица размера .

Задача (1)—(2) обязана своим возникновением следующей задаче оптимизации: найти управление , на котором реализуется минимум функционала

при условии, что состояние управляемой системы является решением системы уравнений з частными производными

,

удовлетворяет начальному условию  и краевым условиям ,

,

где — мерные векторнозначные функции , ,  заданы, — мерная векторнозначная функция  должна быть найдена. По аналогии с конечномерным случаем первое уравнение системы (1) естественно назвать матричным дифференциальным уравнением Риккати с частными производными [7].

3. Основные свойства матричного дифференциального уравнения Риккати с частными производными

Рассмотрим следующее матричное уравнение

 (3)

с дополнительными условиями

                                                            (4)

и

.                                                                         (5)

Предположим, что задача (3)—(5) имеет единственное решение. Если в уравнении (3) выполнить операцию транспонирования, то получим

 (6)

Из условия (4) имеем . Поэтому и, следовательно,

 . (7)

Кроме того, в силу симметричности матрицы имеем

.                                                         (8)

Подставляя (7) в (6) и принимая во внимание равенство (8), видим, что и  являются решениями одной и той же задачи (3) — (5). В силу единственности решения этой задачи приходим к выводу, что . Таким образом, доказано следующее утверждение.

Теорема 1. Если задача (3)—(5) имеет единственное решение, то тогда справедливо равенство , то — есть для каждой упорядоченной фиксированной пары  где  решение  является симметрической матрицей порядка .

Теорема 2. Решение задачи (3) — (5) можно представить в следующем виде

,                                                      (9)

где: функции  и удовлетворяют системе уравнений

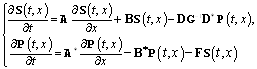                              (10)

и дополнительному условию

                                                              (11)

при условии, что матричнозначная функция  существует.

Доказательство. Ищем решение уравнения (3) в виде произведения

,                                                                         (12)

где:  и  — пока неизвестные функции. Непосредственно из соотношения (12) имеем

                                         (13)

и

.                                        (14)

Подставляя (12), (13) и (14) в уравнение (3), получим

. (15)

Теперь предположим, что существует матричнозначная функция . После умножения справа уравнения (7) на матрицу  имеем

. (16)

Уравнение (16) можно преобразовать следующим образом

,                            (17)

поскольку имеет место равенство , и, поэтому, справедливо также и равенство . Очевидно, что уравнение (9) переписать так

.                                                           (18)

Равенство (18) будет иметь место, если одновременно выполняются следующие два равенства

                             (19)

и

. (20)

Дальше в уравнениях (19) и (20) сделаем замену . Поскольку справедливы следующие равенства

 и ,

то с учетом этих замечаний совокупность уравнений (19) и (20) можно переписать в виде системы уравнений

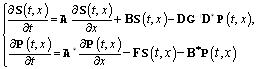 .                            (21)

Наконец, из равенств и  получаем , что и требовалось доказать.

Теорема 3. Если рассмотреть блочную матрицу размера 

 ,                                                 (22)

то систему уравнений (21) можно записать в следующем виде

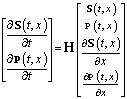,                                                        (23)

где  — квадратная матрица размера , все элементы которой равны нулю.

Доказательство. Действительно, путем непосредственного вычисления находим

Подобным образом устанавливается и следующее утверждение.

Теорема 4. С помощью матрицы (15) систему (1) можно записать в блочной форме

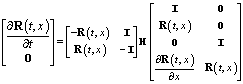,                                 (24)

где — единичная матрица размера ,  — квадратная матрица размера , все элементы которой равны нулю.

Доказательство. В самом деле, имеем

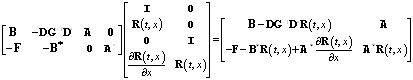
Дальше находим

.

Таким образом, окончательно получим

, .

Это означает, что равенство (24) доказано.

Теорема 5. Пусть функция  есть частным решением уравнения (3) 

Если — некоторое другое решение уравнения (3), отличное от , то функция  удовлетворяет следующему матричному уравнению Бернулли с частными производными

,   (25)

где: , . При этом выполняется равенство .

Доказательство. Из равенства  непосредственно имеем  и . Подставляя эти выражения в уравнение (3), получим

. (26)

Поскольку

 ,

то уравнение (26) перепишется так

.

Введем обозначение . Тогда  . В результате окончательно имеем

.

Кроме того, из равенств  и  следует также, что . Это означает, что теорема 5 доказана.

Теорема 6. С помощью замены  уравнение (25) сводится

к линейному уравнению .

Доказательство.

 Имеем и . Подставляя эти выражения в уравнение (25), получим

.                  (27)

Поскольку , то это означает, что . Следовательно, равенство (27) будет иметь вид

.

Умножая последнее равенство слева на матрицу , получим

.

После умножения этого уравнения справа на матрицу  окончательно имеем

.                       (28)

Таким образом, уравнение (28) является линейным относительно неизвестной функции . При этом выполняется равенство . Пусть известно частное решение  уравнения (28). Тогда это уравнение можно свести к однородному уравнению, если выполнить замену . 

Соответствующее однородное уравнение имеет вид

.                                  (29)

Очевидно, что дополнительно имеет место равенство .

Решение уравнения (29) ищем в виде следующего произведения , где — произвольная постоянная матрицы размера ,  и — неизвестные матрицы такого же размера. Отсюда следует, что

И      .

Подставляя эти выражения в уравнение (29), в результате имеем

.

Перепишем это уравнение следующим образом

. (30)

Поскольку , то , и

, то уравнение (30)

примет вид

.

Это равенство выполняется, если одновременно выполняются следующие два равенства

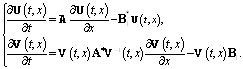                                            (31)

Умножая второе уравнение системы (31) сперва на матрицу  слева, потом на эту же матрицу справа, получим

.      (32)

Дальше сделаем замену . Поскольку

и , то

уравнение (32) примет вид . Таким образом, система (31) примет вид

                                                              (33)

Уравнение (3) можно записать в симметрической форме. Действительно, из условия  следует, что . Это значит, что  и

.

Поэтому уравнение (3) можно переписать так

 (34)

Уравнение (34) естественным образом порождает следующую блочную матрицу

                                                  (35)

размера .

Теорема 7. С помощью матрицы (35) уравнение (34) можно представить таким образом

.

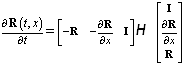Доказательство. С помощью непосредственного вычисления находим

,

,

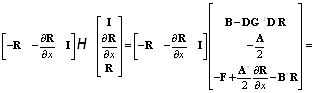
что и требовалось доказать.

Список литературы:

1. Андреев Ю. А. Управление конечномерными линейными объектами. — М.: Наука, 1976. — 424 с.
2. Бублик Б. Н., Кириченко Н. Ф. Основы теории управления. — Киев, издательское объединение «Вища школа», 1975. — 328 с.
3. Егоров А. И. Уравнение Риккати. — М.: ФИЗМАТЛИТ, 2001. — 320 с.
4. Захар — Иткин М. Х. Методы численного решения граничных задач для матричных телеграфных уравнений. // Электричество — 1971. — Том 2 — с. 33—37.
5. Захар — Иткин М. Х. Матричное дифференциальное уравнение Риккати и полугруппа дробно — линейных преобразований. // УМН. — 1973. — Том XXVIII, вып.3 (171) — с. 83—120.
6. Зеликин М. И. Однородные пространства и уравнение Риккати в вариационном исчислении. — М.: Изд — во «Факториал», 1998. — 351 с.
7. Копец М. М. Оптимальное управление объектом, описываемым сингулярной системой линейных уравнений с частными производными. // «Математика и информационные технологии в современном мире», материалы международной заочной научно — практической конференции. — Новосибирск, 2011. — С. 5— 17.
8. Лионс Ж.—Л. Оптимальное управление системами, описываемыми уравнениями с частными производными. — М.: Мир, 1972. — 414 с.
9. Лурье К. А. Оптимальное управление в задачах математической физики. М.: Наука, 1975. — 480 с.
10. Ройтенберг Я. Н. Автоматическое управление. — М.: Наука, 1978. — 551 с.
11. Bittanti S., Laub A. J., Willems J. C. The Riccati equation. New York: Springer — Verlag, 1991.
12. Curtain R. F., Pritchard A. J. Functional analysis in modern applied mathematics. — Academic press: London — New York — San Francisco. — 1977. — 330 p.
13. Lancaster P., Rodman L. Algebraic Riccati equation. — Oxford University Press. — 1995. — 504 p.
14. Riccati J. Animadversationes in aequationes differentiales secondi gradus. // Actorum eruditorum quae Lipsiare publicantur. — 1724. — Supplementa 8, — p. 66—73.