ИССЛЕДОВАНИЕ ОДНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ КОНКУРЕНЦИИ ТРЕХ ПОПУЛЯЦИЙ

Шестакова Татьяна Петровна

cтарший преподаватель, СВФУ, г. Якутск

E-mail: shestak80@mail.ru

В данной работе проводится исследование математической модели конкуренции трех популяций, объясняющих сосуществование различных популяций в природе. За основу исследования взято уравнение Лотки-Вольтерра (1)

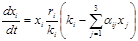 (i=1,2,3),                                    (1)

где rj   - удельная скорость роста, kj - емкость среды i– того вида при отсутствии конкурента (i=1, 2, 3), aij  - положительные безразмерные коэффициенты служат мерой относительного влияния видов друг на друга.

 Путем проведения некоторых преобразований и ввода новых параметров в системе уравнений (1), приходим к более простой математической модели конкуренции трех популяций вида (2), зависящей от трех параметров.

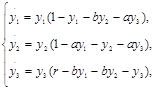                                                 (2)

где b, a, r   –положительные постоянные; a, b  –характеризуют конкуренцию между видами, r   – коэффициент прироста третьего вида. Первый и второй вид имеют одинаковый коэффициент прироста, а коэффициент прироста третьего вида отличен от него.

Задачей работы является, во-первых, выяснить при каких параметрах существует состояние равновесия с положительными координатами и найти условия устойчивого сосуществования трех видов; во-вторых, провести исследование численных методов и построить алгоритмы численного решения модели, с учетом условий асимптотической устойчивости и неустойчивости состояния равновесия; в-третьих, основываясь на результаты графического анализа поведения численных решений уравнений модели (2), определить вымирание одного или более видов, либо сосуществование видов.

 Состоянием равновесия является точка 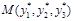, где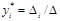  

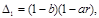
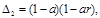
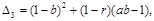
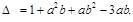
Существуют два возможных случая, при которых состояние равновесия имеет положительные координаты (при 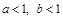 или при 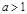, 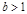). Были получены следующие теоремы [2].

Теорема 1.Если 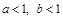, 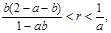то существует состояние равновесия М с положительными координатами и оно асимптотически устойчиво.

При доказательстве теорем используются условия Рауса-Гурвица об отрицательности действительных частей корней характеристического уравнения 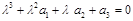, где a₁  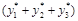=, a₂  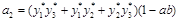=, a₃ =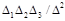

Доказательство: При 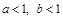 следует, что 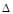>0, a₃ >0, a₂ >0 . Представим условие  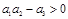в виде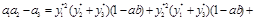

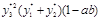 это возможно при выполнении условий теоремы, что и требовалось доказать.

Аналогично доказывается теорема 2.

Теорема 2. Если 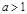, b > 1  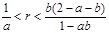то существует состояние равновесия с положительными координатами и оно неустойчиво.

Состояние равновесия неустойчиво, так как не выполняется одно из условий Рауса-Гурвица.

В биологическом смысле теоремы 1 и 2 означают, что в случаях, когда были получены асимптотическая устойчивость состояния равновесия, все виды сосуществуют, так как их взаимное отрицательное влияние достаточно мало, чем коэффициент внутривидовой конкуренции, а когда состояние равновесия неустойчиво возможно вымирание одного или более видов или же переселение на другую территорию.

Были рассмотрены три численных метода решения поставленных задач, проведено исследование устойчивости и погрешности предлагаемых вычислительных схем, наиболее точным из рассмотренных методов был признан метод Рунге-Кутта 4 порядка. Численные решения исследуемой модели изображаются в виде интегральной кривой, описывающей динамику развития трех видов в трехмерном пространстве системы (2) при заданных параметрах, где величины 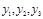, Т являются безразмерными и графика описывающего динамику развития трехвидового сообщества в зависимости от времени. С помощью графического анализа численных решений, можно выяснить какой именно вид или виды не выдерживая, конкуренции идут на вымирание или происходит сосуществование видов, что было затруднительно определить в теоретической части исследования.

Рассмотрим случай асимптотической устойчивости. Приведем некоторые значения параметров удовлетворяющих условиям теоремы 1.

Пример 1.   .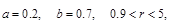

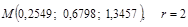Анализ поведения полученных решений показывает, что из любого начального состояния с положительными плотностями, система с течением времени переходит в состояние равновесия 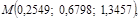 т. е. все виды сосуществуют с друг с другом. Соответствующие графики изображены на рис. 1 и рис. 2.

Рассмотрим случай, когда состояние равновесия неустойчиво, т. е идет вымирание один или более видов.

Пример 2. .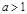, b > 1 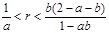, когда

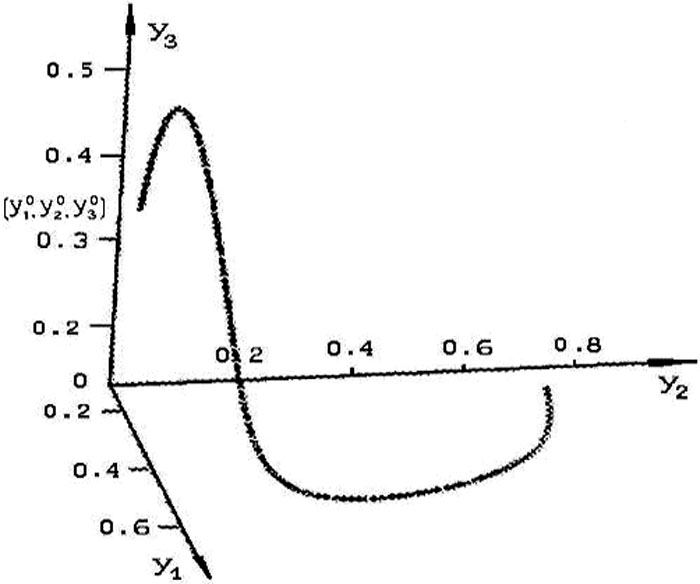
Рис. 1 Интегральная кривая системы (1) изображенная в трехмерном пространстве безразмерных переменных y₁, y₂, y₃, при асимптотической устойчивости состояния равновесия.

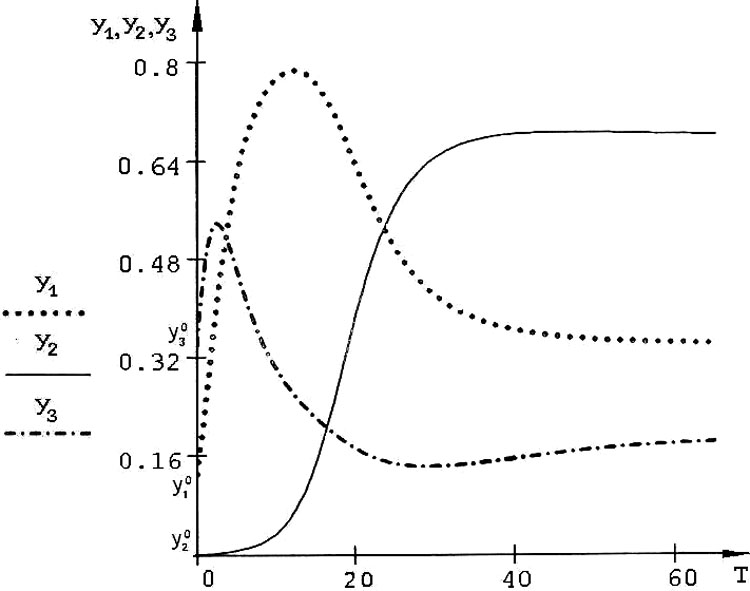
Рис. 2 График отношений видов в зависимости от времени при асимптотической устойчивости состояния равновесия.

В данном примере численные решения системы (2) показывают, что если начальные данные удовлетворяют неравенству , i=1, 2, 3, то первый и второй виды подавляют третий вид, вследствие чего он идет на вымирание. Соответствующие графики изображены на рис. 3 и рис. 4.

Результаты данной работы могут быть использованы для облегчения работы экологам и биологам, при создании заповедников, резерватов и т. д., где наблюдается конкуренция трех популяций, а также для студентов интересующихся проблемами современной экологии.

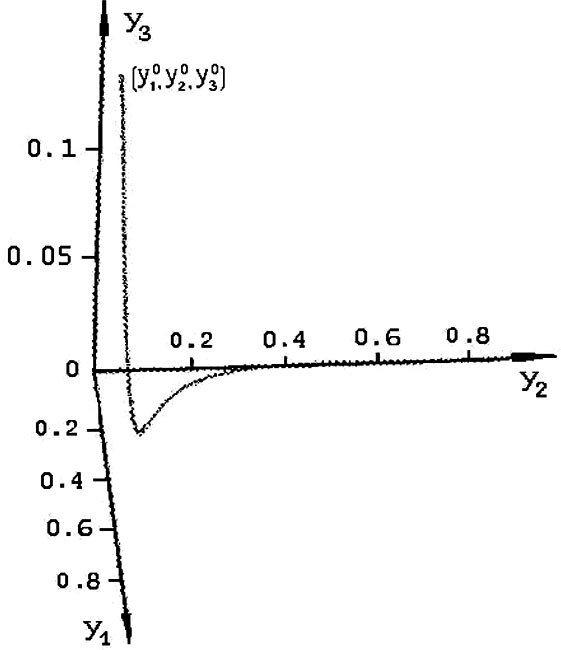
Рис. 3. Интегральная кривая системы (4), изображенная в трехмерном пространстве безразмерных переменных y₁, y₂, y₃, при неустойчивости состояния равновесия, в случае 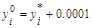, i=1, 2, 3.

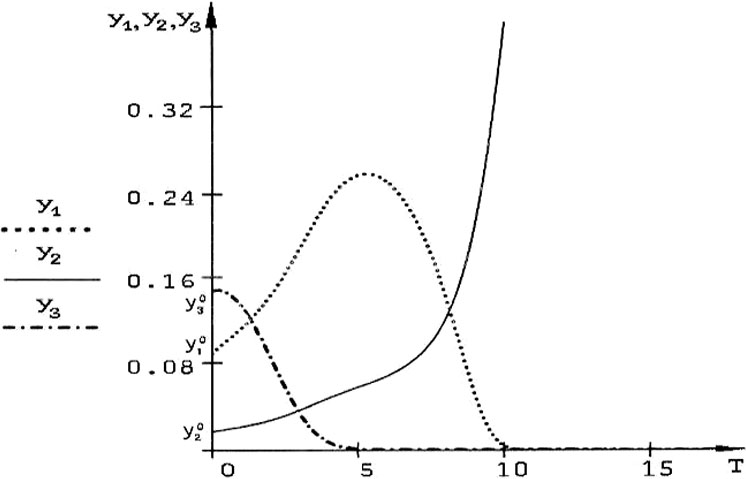
Рис. 4. График отношений видов в зависимости от времени при неустойчивости состояния равновесия, вслучае, когда

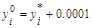  , i=1, 2, 3.

Список литературы:

1. Васильев М. Д., Софронов Е. Т. Параметрическая модель конкуренции в экологии. // Математические заметки ЯГУ, 2000. т. 7, в. 1. С. 4—10.
2. Шестакова Т. П. Исследование трех математических моделей конкуренции трех видов. // сборник статей . VIIЛаврентьевские чтения. РС(Я).- 2004 т. 1. С. 68—76.