Статья опубликована в рамках: XXXV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 05 октября 2015 г.)
Наука: Физика
Секция: Физика конденсированного состояния
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
АВТОМАТИЗАЦИЯ МЕТОДА СЛАБЫХ СИНУСОИДАЛЬНЫХ ПОЛЕЙ С СИНУСОИДАЛЬНОЙ МОДУЛЯЦИЕЙ АМПЛИТУДЫ ДЛЯ ЭЛЕКТРО-ОПТИЧЕСКИХ ИССЛЕДОВАНИЙ ДИСПЕРСНЫХ СИСТЕМ
Войтылов Алексей Владиславович
канд. физ.-мат. наук, старший научный сотрудник
Санкт-Петербургского Государственного Университета,
РФ, г. Санкт-Петербург
E-mail: voivv@mail.ru
Петров Михаил Павлович
канд. физ.-мат. наук, старший преподаватель
Санкт-Петербургского Государственного Университета,
РФ, г. Санкт-Петербург
E-mail: mihaeles@list.ru
Трусов Анатолий Анатольевич
д-р физ.-мат. наук, зав. каф.молекулярной биофизики
Санкт-Петербургского Государственного Университета,
РФ, г. Санкт-Петербург
E-mail: trusov@mail.ru
Войтылов Владислав Викторович
д-р физ.-мат. наук, профессор
Санкт-Петербургского Государственного Университета,
РФ, г. Санкт-Петербург
E-mail: vojtylov@gmail.com
Клемешев Сергей Алексеевич
инженер
Санкт-Петербургского Государственного Университета,
РФ, г. Санкт-Петербург
AUTOMATION OF WEAK SINE SHAPED SINE MODULATED FIELDS TECHNIQUE OF ELECTO-OPTICAL STUDY OF DISPERSE SYSTEMS
Alexey Voitylov
candidate of science, senior researcher at
Saint Petersburg State University,
Russia, Saint-Petersburg
Mikhail Petrov
candidate of science, senior lecturer at
Saint Petersburg State University,
Russia, Saint-Petersburg
Anatoly Trusov
doctor of science, professor at
Saint Petersburg State University,
Russia, Saint-Petersburg
Vladislav Vojtylov
doctor of science, professor at
Saint Petersburg State University,
Russia, Saint-Petersburg
Sergey Klemeshev
engineer at
Saint Petersburg State University,
Russia, Saint-Petersburg
АННОТАЦИЯ
В настоящей работе разработаны методики обработки экспериментальных данных электрооптического метода исследования дисперсных систем с применением синусоидальных электрических полей с синусоидальной модуляцией. Показано, что применение разработанных автоматизированных методик позволяет определять размеры частиц в дисперсной фазе этим методом даже в случае наличия в исследуемом растворе частиц разного размера. Представленные экспериментальные результаты исследования водного коллоида алмаза этим метод подтверждают надежность разработанных алгоритмов.
ABSTRACT
In this paper we present the development of an algorithm of experimental data processing of electro-optical method of study of disperse systems using sine-shaped sine-modulated electric fields. It is shown that the use of robust automated techniques allows to determine size of particles in disperse medium using this method even in the case of disperse systems with particles of different sizes. The presented experimental results of study of aqueous colloid of diamond confirm the robustness of the developed algorithms.
Ключевые слова: электрооптический эффект; распределение по размерам; частицы алмаза;
Keywords: Electro-optical effect; distribution of particle sizes; Diamond particles
Введение
Электрооптические методы используются для исследования дисперсных систем с размерами частиц от нескольких нанометров до нескольких микрон [7]. В отличие от широко распространенного метода динамического светорассеяния [2], с помощью электрооптических методов можно получать не только значения размеров частиц в дисперсной фазе, но и информацию, характеризующую поверхностные свойства частиц, например, значения анизотропии полярзуемости и поверхностной проводимости. Разработанные методы обработки экспериментальных данных электрооптических эффектов [1] позволяют определять не только средние значения размеров и анизотропии поляризуемости, но и функции распределения по ним частиц в дисперсной фазе. В том случае, если исследуемая система допускает приложение электрических полей большой величины (например, не является электропроводной) и исследовательская аппаратура допускает создание насыщенной ориентации частиц, можно применять метод коротких импульсов [3; 4] или исследовать стационарные электрооптические эффекты для определения распределений частиц по размерам и анизотропии поляризуемости. В случае, если исследуемая система является электропроводной или не допускает создание насыщенной ориентации частиц, можно использовать электрооптические эффекты в слабых полях [5] для определения размеров частиц в исследуемой системе и функции распределения частиц в системе по размерам.
В данной работе авторы развивают методику обработки экспериментальных данных электрооптического метода исследования дисперсных систем с применением синусоидальных электрических полей с синусоидальной модуляцией для автоматизации эксперимента и надежного определения дисперсионных зависимостей электрооптического эффекта. Такой подход позволит более точно определять функцию распределения частиц по размерам, а значит исследовать динамику дисперсных систем, состоящих из нескольких фракций, и механизмы агрегации коллоидных частиц.
Электро-оптические эффекты в слабых синусоидальных полях с синусоидальной модуляцией
Метод исследования электро-оптических эффектов в слабых электрических полях (![]() ) вида
) вида
![]() (1)
(1)
предполагает получение дисперсионной зависимости электрооптического эффекта ![]() , варьируя частоту приложенного к системе электрического поля
, варьируя частоту приложенного к системе электрического поля ![]() и оставляя
и оставляя ![]() постоянной. Теоретическая зависимость
постоянной. Теоретическая зависимость ![]() , описывающая электрооптический эффект в поле такого вида для частиц с заданным размером r и константой вращательной диффузии
, описывающая электрооптический эффект в поле такого вида для частиц с заданным размером r и константой вращательной диффузии ![]() , получена в работе [5]:
, получена в работе [5]:
 (2)
(2)
В том случае, если в исследуемом растворе присутствуют частицы разного размера, экспериментальную дисперсионную зависимость ![]() можно связать с
можно связать с ![]() в (2) следующим выражением
в (2) следующим выражением
 (3)
(3)
где: ![]() — функция распределения частиц в исследуемом растворе по константам вращательной диффузии с дихроическим весом [7],
— функция распределения частиц в исследуемом растворе по константам вращательной диффузии с дихроическим весом [7],
![]() — минимальное и максимальное значение константы вращательной диффузии частиц в исследуемом растворе. Подставляя (2) в (3), можно получить следующую формулу:
— минимальное и максимальное значение константы вращательной диффузии частиц в исследуемом растворе. Подставляя (2) в (3), можно получить следующую формулу:
![]() (4)
(4)
где
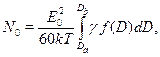 (5)
(5)
 (6)
(6)
 (7)
(7)
Таким образом, определяя ![]() или
или ![]() из
из ![]() , а затем решая уравнение (7) или (8) относительно
, а затем решая уравнение (7) или (8) относительно ![]() можно определить функцию распределения частиц в исследуемом растворе по константам вращательной диффузии
можно определить функцию распределения частиц в исследуемом растворе по константам вращательной диффузии ![]() , а значит и по размерам r.
, а значит и по размерам r.
Автоматизированный метод обработки экспериментальных данных
Процедура экспериментального определения ![]() и
и ![]() с помощью традиционных методик (например, с помощью фигур Лиссажу на экране осциллографа) трудоемка, так как требуется определять значения
с помощью традиционных методик (например, с помощью фигур Лиссажу на экране осциллографа) трудоемка, так как требуется определять значения ![]() и
и ![]() для целого набора частот. Поскольку уравнения (6), (7) — уравнения Фредгольма I рода, решение которых относится к классу некорректных задач, определение
для целого набора частот. Поскольку уравнения (6), (7) — уравнения Фредгольма I рода, решение которых относится к классу некорректных задач, определение ![]() и
и ![]() требуется проводить с максимально возможной точностью. Применять метод Фурье анализа для получения
требуется проводить с максимально возможной точностью. Применять метод Фурье анализа для получения ![]() или
или ![]() из
из ![]() затруднительно, поскольку за время измерения исследуемого эффекта система может измениться (например, вследствие коагуляции частиц). Поэтому для определения зависимостей
затруднительно, поскольку за время измерения исследуемого эффекта система может измениться (например, вследствие коагуляции частиц). Поэтому для определения зависимостей ![]() и
и ![]() разработана методика обработки экспериментальных данных на основе метода наименьших квадратов.
разработана методика обработки экспериментальных данных на основе метода наименьших квадратов.
Для численного определения ![]() ,
, ![]() и
и ![]() из экспериментальной зависимости установившегося электрооптического эффекта от времени
из экспериментальной зависимости установившегося электрооптического эффекта от времени ![]() , измеренной в моменты времени
, измеренной в моменты времени ![]() , составляется функционал
, составляется функционал
![]()
необходимое условие минимума которого
![]() (8)
(8)
Уравнение (8) может быть записано в виде
 (9)
(9)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решением линейного уравнения (9) являются искомые параметры ![]() ,
, ![]() и
и ![]() .
.
Такой способ обработки экспериментальных данных позволяет автоматизировать проведение исследований и повысить точность определения ![]() и
и ![]() , что, в свою очередь, позволяет применить численные методы, описанные в [3] для решения уравнений (6), (7).
, что, в свою очередь, позволяет применить численные методы, описанные в [3] для решения уравнений (6), (7).
Результаты эксперимента
Для проверки предлагаемого метода были проведены экспериментальные исследования водного коллоида алмаза, который приготавливался разбавлением алмазного порошка бидистилированной водой. Полученный таким образом коллоид обладает ярко выраженным дихроизмом в электрическом поле даже при низкой концентрации дисперсной фазы (менее 1 мг вещества на 100 г воды). Коллоид не коагулировал в течение нескольких суток. Как показали данные электронной микрофотографии, частицы алмаза можно считать эллипсоидами с соотношением осей p≃1.5.
Частота ![]() ориентирующего частицы электрического поля была выбрана равной 20 кГц, а
ориентирующего частицы электрического поля была выбрана равной 20 кГц, а ![]() варьировалась от 1 Гц до 2 кГц при
варьировалась от 1 Гц до 2 кГц при ![]() В/см.
В/см.
Дисперсионные кривые ![]() и
и ![]() , полученные описанным выше методом для данного коллоида представлены на Рис. 1. Функции
, полученные описанным выше методом для данного коллоида представлены на Рис. 1. Функции ![]() , где
, где ![]() — дихроический вес частиц алмаза с заданным размером и
— дихроический вес частиц алмаза с заданным размером и ![]() (истинная функция распределения частиц в исследуемом растворе по размерам), рассчитанные при использовании зависимости
(истинная функция распределения частиц в исследуемом растворе по размерам), рассчитанные при использовании зависимости ![]() и уравнения (6), хорошо согласуются с функциями
и уравнения (6), хорошо согласуются с функциями ![]() и
и ![]() , рассчитанными при использовании зависимости
, рассчитанными при использовании зависимости ![]() и уравнения (7). Как видно из рисунка, в исследуемой дисперсной системе присутствуют частицы разного размера, причем, наряду с частицами размером 200 нм (основная фракция в дисперсной фазе) присутствуют также частицы алмаза меньшего размера (70 нм). Эти результаты согласуются с результатами электрооптических исследований коллоида алмаза в сильных электрических полях [3; 6]. Данные агрегаты образуются в растворе, и на микрофотографических снимках отсутствуют.
и уравнения (7). Как видно из рисунка, в исследуемой дисперсной системе присутствуют частицы разного размера, причем, наряду с частицами размером 200 нм (основная фракция в дисперсной фазе) присутствуют также частицы алмаза меньшего размера (70 нм). Эти результаты согласуются с результатами электрооптических исследований коллоида алмаза в сильных электрических полях [3; 6]. Данные агрегаты образуются в растворе, и на микрофотографических снимках отсутствуют.

Рисунок 1. Дисперсионные зависимости электрооптического эффекта N в слабом синусоидальном поле в гидрозоле алмаза и результаты их обработки: 1 — ![]() ; 2 —
; 2 — ![]() ; 3 —
; 3 — ![]() (рассчитана по
(рассчитана по ![]() ); 4 —
); 4 — ![]() (рассчитана по
(рассчитана по ![]() ); 5 —
); 5 — ![]() (рассчитана по
(рассчитана по ![]() ); 6 —
); 6 — ![]() (рассчитана по
(рассчитана по ![]() ).
).
Выводы
Разработанный метод обработки экспериментальных данных электрооптических исследований позволяет надежно определять дисперсионные зависимости электрооптического эффекта в слабом синусоидальном поле. Проведенные экспериментальные исследования водного коллоида алмаза показывают, что использование автоматизированного метода исследования позволяет надежно определять размеры частиц в исследуемой системе даже в случае полидисперсных систем и дисперсных систем, содержащих агрегаты частиц.
Список литературы:
- Babadzanjanz L, Voitylov A. Numerical methods for inverse problems in electrooptics of polydisperse colloids. Colloids Surf B Biointerfaces — 2007. — Vol. 56, — № (1—2). — P. 121—125.
- Berne B.J., Pecora R. Dynamic light scattering: with applications to Chemistry, Biology and Physics. Dover Publications Inc., 2000, — 376 p.
- Klemeshev S.A., Petrov M.P., Trusov A.A., Voitylov A.V. Electrooptical effects in colloid systems subjected to short pulses of strong electric field.// Journal of Physics — Condensed matter. — 2010. — Vol. 22, — № 49. — P. 12—22.
- Klemeshev S.A., Petrov M.P., Shalygin A.K., Trusov A.A., Voitylov A.V. Electro-optical effects in disperse systems in strong electric fields of arbitrary shape. Colloids and Surfaces A: Physicochemical and Engineering Aspects. — 2014. — Vol. 456. — P. 114—119.
- Trusov A.A., Vojtylov V.V., and Zernova T.Yu. Electrooptic and conductometric effects in colloids and suspensions in sinusoidally amplitude modulated sine-shaped electric fields. Colloids and Surfaces A: Physicochemical and Engineering Aspects — 2002. — Vol. 201.1. — P. 31—40.
- Vojtylov V.V., Klemeshev S.A., Petrov M.P., Trusov A.A. Light scattering by diamond and graphite nanodisperse systems with their particles orientationally ordered in an electric field. Optics and Spectroscopy, — 2013. — Vol. 114(3). — P. 432—439.
- Vojtylov V.V., Trusov A.A., Spartakov A.A., and Voitylov A.V, Electro-Optics of Polydisperse Colloids. // Chap. 7 in "Molecular and Colloidal Electro-optics", Ed. by Stoyl P . Stoylov and Maria Stoimenova, London, N.Y.: CRC Press — 2006. — P. 193—227.
дипломов


Оставить комментарий