Статья опубликована в рамках: XXXII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 26 марта 2014 г.)
Наука: Технические науки
Секция: Нанотехнологии и наноматериалы
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОПТИЧЕСКИЕ И ЭЛЕКТРООПТИЧЕСКИЕ СВОЙСТВА ВОДНЫХ ВЗВЕСЕЙ НАНОЧАСТИЦ АЛМАЗА
Войтылов Алексей Владиславович
канд. физ.-мат. наук, старший преподаватель Санкт-Петербургского Государственного Университета, РФ, г. Санкт-Петербург
Петров Михаил Павлович
аспирант Санкт-Петербургского Государственного Университета, РФ, г. Санкт-Петербург
Трусов Анатолий Анатольевич
д-р физ.-мат. наук, зав. каф.молекулярной биофизики Санкт-Петербургского Государственного Университета, РФ, г. Санкт-Петербург
Войтылов Владислав Викторович
д-р физ.-мат. наук, профессор Санкт-Петербургского Государственного Университета, РФ, г. Санкт-Петербург
Клемешев Сергей Алексеевич
инженер Санкт-Петербургского Государственного Университета, РФ, г. Санкт- Петербург
OPTICAL AND ELECTRO-OPTICAL PROPERTIES OF AQUEOUS SUSPENSIONS OF DIAMOND NANOPARTICLES
Alexey Voitylov
candidate of science, senior lecturer at Saint Petersburg State University, Russia Saint-Petersburg
Mikhail Petrov
post-graduate student at Saint Petersburg State University, Russia Saint-Petersburg
Anatoly Trusov
doctor of science, head of molecular biophysics department at Saint Petersburg State University, Russia Saint-Petersburg
Vladislav Vojtylov
doctor of science, professor at Saint Petersburg State University, Russia Saint-Petersburg
Sergey Klemeshev
engineer at Saint Petersburg State University, Russia Saint-Petersburg
АННОТАЦИЯ
В настоящей работе рассмотрены оптические свойства водных взвесей наночастиц алмаза размером от 100 до 1000 нм. Показано, что приложение электрического поля меняет интенсивности прошедшего и рассеянного света, а также степень деполяризации рассянного света. Исследования электрооптических эффектов в взвеси наночастиц алмаза позволили определить функции распределения частиц по размерам и значениям анизотропии поляризуемости, связанной с их анизотропией формы и удельной поверхностной проводимостью частиц.
ABSTRACT
In this paper we consider the optical properties of aqueous suspensions of diamond nanoparticles with size from 100 to 1000 nm. It is shown that the application f electric field changes the light intensity of the scattered and transmitted light, as well as the depolarization of scattered light. The study of electro-optical effects in the suspension of nanoparticles of diamond allowed to determine the distribution functions of particles on size and polarizability anisotropy, which is connected to to particle shape anisotropy and specific surface conductivity.
Ключевые слова: частицы алмаза; светорассеяние; деполяризация рассеянного света; электрооптический эффект; распределение по размерам; поверхностная проводимость
Keywords: Diamond particles; light scattering; depolarization of scattered light; Electro-optical effect; distribution of particle sizes; surface conductivity
Введение
Частицы алмаза субмикронного размера широко используются в целом ряде отраслей промышленности, обладая высокой жесткостью и практически не образуя агрегатов, в которых частицы были бы связаны силами притяжения большой величины. Наиболее часто они употребляются в шлифовальных пастах и иных дисперсных системах, которые могут быть получены разведением дисперсной фазы в водной среде. Однако во всех случаях требуется контроль размеров частиц дисперсной фазы алмаза. Прямой контроль размеров и формы частиц дисперсной фазы проводится электронно-микроскопическими наблюдениями, требующими больших затрат времени, связанных с получением разбавленной коллоидной суспензии алмаза, высушиванием ее, закрепляя на подложке отдельные частицы а не сгустки из них. Такой метод трудно использовать для непрерывного и не дорогостоящего анализа дисперсной фазы алмаза. Для анализа дисперсной фазы можно использовать оптические свойства суспензий алмаза, изучая, например, взвесь частиц алмаза в воде [8]. Такие взвеси существенно рассеивают свет, что делает их диагностику методами светорассеяния легкой и точной. Если размеры частиц не превышают 100 нм, то для определения размеров и распределения по ним вполне пригоден метод динамического светорассеяния, подробно рассмотренный в монографии [6]. Если же размеры частиц более 100 нм, то рассеяние света этим методом менее надежно. А именно, автокорреляционные функции интенсивности существенно меняются при изменении поляризации падающего или рассеянного света. Использование метода динамического светорассеяния осложняется тем, что флуктуации рассеяния, обусловленные поступательным движением частиц одних размеров, накладываются на флуктуации вращательного движения частиц другого размера, что делает сложным решение обратных задач динамического светорассеяния.
В данной работе представлены результаты исследования оптических свойств водных систем, в которых взвешены частицы алмаза, соизмеримые с длиной световой волны. Проведен анализ статического рассеяния света, требующего более простой и дешевой аппаратуры, чем в случае динамического светорассеяния. Исследовано также влияние электрического поля, которое меняет оптические свойства системы, только по причине их ориентационной упорядоченности и вращательного движения. Это существенно упрощает определение характеристик частиц, как геометрических, так и электрических.
Техника эксперимента и измеряемые величины
При определении рефракции исследуемых систем использовался рефрактометр Релея, в котором показатель преломления воды сравнивался с показателем преломления исследуемых систем.
Для исследований рассеяния разработана и создана экспериментальная установка, схема оптической части которой представлена на Рис. 1а.
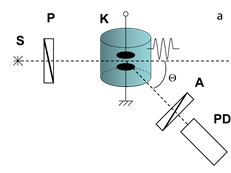
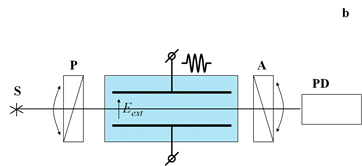
Рисунок 1. Оптические схемы экспериментальных установок для исследования рассеяния (а) и мутности (b ). S — источник света; P — поляризатор; К — кювета с электродами и рассеивающей свет системой; А — анализатор; PD — фотоприемник
Луч падающего света создавался полупроводниковым лазером с длиной волны 635 нм. Направление линейной поляризации падающего и принимаемого фотоприемником лучей определялось поляпризатором и анализатором. Плоскость поляризации горизонтальна, а прикладываемое к кювете синусоидальное поле вертикально. Поле прикладывалось импульсами длительностью не более 0,1 с, имело частоту 5 кГц, величина эффективной напряженности поля могла меняться от нуля до 1200 В/см. Угол расходимости регистрируемого рассеянного пучка света не превышал ![]() , угол рассеяния задавался с точностью
, угол рассеяния задавался с точностью ![]() . Данная установка позволяла измерять интенсивности рассеянного света
. Данная установка позволяла измерять интенсивности рассеянного света ![]() и
и ![]() поляризованного вертикально и горизонтально, соответственно, при вертикальной
поляризованного вертикально и горизонтально, соответственно, при вертикальной ![]() и
и ![]() горизонтальной поляризации падающего света, отмеченной подстрочными индексами. Если измерения проводились под воздействием на систему электрического поля, то использован надстрочный индекс
горизонтальной поляризации падающего света, отмеченной подстрочными индексами. Если измерения проводились под воздействием на систему электрического поля, то использован надстрочный индекс ![]() .
.
При измерении мутности круглая кювета заменялась на прямоугольную ячейку Керра, а угол рассеяния ![]() выставлялся равным нулю, как изображено на Рис. 1б. В этом случае измерялись интенсивности прошедшего света
выставлялся равным нулю, как изображено на Рис. 1б. В этом случае измерялись интенсивности прошедшего света ![]() и
и ![]() , для которого падающий свет интенсивности
, для которого падающий свет интенсивности ![]() поляризован вертикально и горизонтально. В этих измерениях плоскости поляризации падающего и прошедшего света совпадали.
поляризован вертикально и горизонтально. В этих измерениях плоскости поляризации падающего и прошедшего света совпадали.
Характеристики прошедшего и рассеянного света
Исследования оптических характеристик водных растворов частиц синтетического алмаза проводились при различных концентрациях частиц. Согласно снимкам таких частиц на подложке, выполненным при помощи электронного микроскопа, наиболее вероятные размеры частиц лежали в области 400—450 нм, но также встречались частицы с размерами менее 100 и более 700 нм. Частицы слабо вытянуты и среднее отношение наибольшего к наименьшему размеру частицы можно считать равным 1,2—1,25. Определить, имеются ли агрегаты прочно соединенных частиц, не удавалось.
Мутность исследуемых систем зависит от интенсивности прошедшего ячейку Керра света. Ее можно охарактеризовать константами ослабления света:
![]() ,
, ![]() ,
, ![]() и
и ![]() . (1)
. (1)
Здесь ![]() — длина ячейки Керра. Без приложения поля система изотропна и
— длина ячейки Керра. Без приложения поля система изотропна и ![]() , ориентация частиц в поле делает систему анизотропной и
, ориентация частиц в поле делает систему анизотропной и ![]() .
.
При увеличении концентрации взвешенных частиц интенсивность света, проходящего ячейку Керра длиной 5 см уменьшалась более, чем на десятичный порядок, при этом константа ![]() возрастала от нуля до значения
возрастала от нуля до значения ![]() см-1, однако отклонения показателя преломления систем с частицами от показателя преломления воды не наблюдалось. В исследованиях показателя преломления анализировались: угол преломления света призмой, заполненной исследуемой системой; угол полного внутреннего отражения; сдвиг интерференционных полос в рефрактометре Релея. Интерференционный метод наиболее точен и позволял определять изменения показателя преломления систем с точностью
см-1, однако отклонения показателя преломления систем с частицами от показателя преломления воды не наблюдалось. В исследованиях показателя преломления анализировались: угол преломления света призмой, заполненной исследуемой системой; угол полного внутреннего отражения; сдвиг интерференционных полос в рефрактометре Релея. Интерференционный метод наиболее точен и позволял определять изменения показателя преломления систем с точностью ![]() , однако и при использовании этого метода не удалось зарегистрировать отличие показателя преломления раствора от показателя преломления воды. Это делало неэффективным использование рефрактометрического метода для анализа частиц, а их характеристики следует связывать с особенностями рассеяния света взвесями.
, однако и при использовании этого метода не удалось зарегистрировать отличие показателя преломления раствора от показателя преломления воды. Это делало неэффективным использование рефрактометрического метода для анализа частиц, а их характеристики следует связывать с особенностями рассеяния света взвесями.
Такие характеристики могут быть получены при исследовании индикатрис рассеянного света разных поляризаций и степени деполяризации при разных углах рассеяния. Были измерены индикатрисы светорассеяния, а также степени деполяризации рассеянного света ![]() и
и ![]() . Угловые зависимости
. Угловые зависимости ![]() ,
, ![]()
![]() и
и ![]() представлены на Рис. 2. Для деполяризованных компонент рассеянного света в системах с хаотической концентрацией частиц проверено, что выполняется теорема обратимости Релея, а именно
представлены на Рис. 2. Для деполяризованных компонент рассеянного света в системах с хаотической концентрацией частиц проверено, что выполняется теорема обратимости Релея, а именно ![]() при всех углах рассеяния и не зависимо от характера рассеяния света частицами. В электрическом поле частицы в растворе ориентируются и
при всех углах рассеяния и не зависимо от характера рассеяния света частицами. В электрическом поле частицы в растворе ориентируются и ![]() . Для исследованной системы
. Для исследованной системы ![]() и
и ![]() при всех углах рассеяния, а
при всех углах рассеяния, а ![]() , и
, и ![]() . Независимость
. Независимость ![]() от величины поля согласуется с тем, что для частиц, соизмеримых с длиной волны света,
от величины поля согласуется с тем, что для частиц, соизмеримых с длиной волны света, ![]() главным образам определяется квадрупольным рассеянием, которое практически не меняются при ориентации столь слабо вытянутых частиц алмаза. Существенное квадрупольное рассеяние света частицами также подтверждают зависимости
главным образам определяется квадрупольным рассеянием, которое практически не меняются при ориентации столь слабо вытянутых частиц алмаза. Существенное квадрупольное рассеяние света частицами также подтверждают зависимости ![]() и
и ![]() от угла рассеяния.
от угла рассеяния.
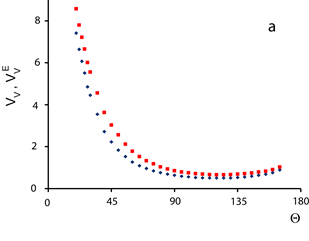
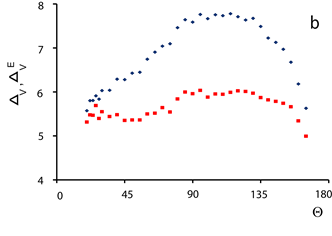
Рисунок 2. Индикатрисы (а) и степень деполяризации (b ) рассеянного света частицами алмаза при хаотической (♦) и полной (■) ориентации частиц в поле
В выше рассмотренных исследованиях величины, измеренные в поле отвечают насыщенной ориентации частиц вдоль поля , когда увеличение поля перестает влиять на их изменение.
Ассиметрия индикатрис светорассеяния, может быть использована для определения размеров частиц [4]. Для частиц алмаза ![]() и, если полагать частицы сферами одного диаметра, то их диаметр
и, если полагать частицы сферами одного диаметра, то их диаметр ![]() мкм. Полученный размер частиц меньше наиболее вероятного, определенных при помощи электронного микроскопа. Это связано с использованием монодисперсного приближения к полидисперсной системе. Более детальную информацию о частицах можно получить, исследуя изменения оптических характеристик систем в полях разной напряженности и после выключения поля. Такие исследования позволяют учесть полидисперсность систем.
мкм. Полученный размер частиц меньше наиболее вероятного, определенных при помощи электронного микроскопа. Это связано с использованием монодисперсного приближения к полидисперсной системе. Более детальную информацию о частицах можно получить, исследуя изменения оптических характеристик систем в полях разной напряженности и после выключения поля. Такие исследования позволяют учесть полидисперсность систем.
Изучение полидисперсности и поляризуемости частиц алмаза
Здесь мы более детально остановимся на двух характеристиках, возникающих при создании ориентационной упорядоченности частиц. Первая — относительное изменение интенсивности рассеянного света, вторая — разность коэффициентов экстинкции. Для падающего и рассеянного света, поляризованных вертикально можем написать
![]() , (2)
, (2)
а зависимость мутности от направления поляризации падающего света характеризует дихроизм, обусловленный рассеянием системой света
![]() . (3)
. (3)
В монодисперсном приближении эти характеристики меняются пропорционально функции ![]() ориентационного порядка,
ориентационного порядка, ![]() и
и ![]() , которая равна нулю при хаотической и единице при полной ориентациях частиц. Здесь оптические веса
, которая равна нулю при хаотической и единице при полной ориентациях частиц. Здесь оптические веса ![]() и
и ![]() соответствуют значениям
соответствуют значениям ![]() и
и ![]() при насыщенной ориентации частиц. Величина
при насыщенной ориентации частиц. Величина ![]() зависит от угла рассеяния. Если частицы ориентировать синусоидальным полем радиочастоты, то степень ориентационного порядка частиц при их стационарной ориентации
зависит от угла рассеяния. Если частицы ориентировать синусоидальным полем радиочастоты, то степень ориентационного порядка частиц при их стационарной ориентации ![]() определяется их анизотропией электрической поляризуемости
определяется их анизотропией электрической поляризуемости ![]() и напряженностью
и напряженностью ![]() эффективного поля [9]
эффективного поля [9]
![]() . (4)
. (4)
При релаксации из состояния насыщенной ориентации частиц функция ![]() ориентационного порядка зависит от времени
ориентационного порядка зависит от времени ![]() и констант вращательной диффузии частиц
и констант вращательной диффузии частиц ![]() [9]
[9]
![]() . (5)
. (5)
Полагая частицы эллипсоидами вращения можно определить анизотропию поляризуемости частиц, как разность ![]() поляризуемостей вдоль и перпендикулярно оси эллипсоида, где [1, 2]
поляризуемостей вдоль и перпендикулярно оси эллипсоида, где [1, 2]
![]() , (6)
, (6)
![]() , (7)
, (7)
Входящие в (6) и (7) ![]() и
и ![]() — полуоси эллипсоида, а коэффициенты
— полуоси эллипсоида, а коэффициенты ![]() ,
, ![]() и с определяются отношением полуосей эллипсоида
и с определяются отношением полуосей эллипсоида ![]() ,
,
![]() ,
,![]() ,
,
![]() ,
, ![]() .
.
Параметр ![]() не зависит от размеров и формы частиц, а определяется отношением удельных поверхностной проводимости
не зависит от размеров и формы частиц, а определяется отношением удельных поверхностной проводимости ![]() к объемной проводимости электролита
к объемной проводимости электролита ![]() , окружающего частицу,
, окружающего частицу, ![]() ,
, ![]() — диэлектрическая проницаемость дисперсионной среды вокруг частиц.
— диэлектрическая проницаемость дисперсионной среды вокруг частиц.
Константу вращательной диффузии, определяющую релаксационные зависимости, также можно выразить через размеры и форму эллипсоида вращения и вязкость среды ![]() [7]
[7]
![]() . (8)
. (8)
В полидисперсной системе при стационарной ориентации частиц на зависимости ![]() и
и ![]() влияет функция распределения частиц по их значениям анизотропии поляризуемости
влияет функция распределения частиц по их значениям анизотропии поляризуемости ![]() . Эти зависимости можно представить соотношениями
. Эти зависимости можно представить соотношениями
![]() , (9)
, (9)
![]() . (10)
. (10)
Кривые релаксации ![]() и
и ![]() зависят от функции распределения частиц по константам их вращательной диффузии
зависят от функции распределения частиц по константам их вращательной диффузии ![]() . Вместо входящего в (6)—(8) произведения
. Вместо входящего в (6)—(8) произведения ![]() можно использовать
можно использовать ![]() , полагая
, полагая ![]() , где
, где ![]() — радиус сферы, объем которой равен объему частицы. Тогда
— радиус сферы, объем которой равен объему частицы. Тогда ![]() является известной функцией
является известной функцией ![]() и
и ![]() , а
, а ![]() — известная функция
— известная функция ![]() ,
,![]() и
и ![]() . Это позволяет ввести функцию распределения частиц по размерам
. Это позволяет ввести функцию распределения частиц по размерам ![]() и связать ее с функциями
и связать ее с функциями ![]() и
и ![]() соотношениями
соотношениями
![]() и
и ![]() . (11)
. (11)
При совместном анализе стационарных эффектов и их релаксации в полидисперсной системе целесообразно использовать функции распределения ![]() . Кривые релаксации можно выразить соотношениями
. Кривые релаксации можно выразить соотношениями
![]() (12)
(12)
![]() (13)
(13)
Соотношения (12) и (13) можно рассматривать как интегральные уравнения для определения функций ![]() и
и ![]() , если экспериментально определены зависимости
, если экспериментально определены зависимости ![]() и
и ![]() . Функции
. Функции ![]() , определенные при разных углах рассеяния, могут несколько различаться между собой и отличаться от функции
, определенные при разных углах рассеяния, могут несколько различаться между собой и отличаться от функции ![]() , так как входящие в них оптические веса
, так как входящие в них оптические веса ![]() и
и ![]() имеют различающиеся зависимости от размеров частиц. Если определена функция распределения
имеют различающиеся зависимости от размеров частиц. Если определена функция распределения ![]() или
или ![]() , то использование соотношений (6) и (7) позволяет рассчитать
, то использование соотношений (6) и (7) позволяет рассчитать ![]() или
или ![]() при заданном параметре
при заданном параметре ![]() . Сопоставление рассчитанных и экспериментально определенных зависимостей позволяет определить истинное значение
. Сопоставление рассчитанных и экспериментально определенных зависимостей позволяет определить истинное значение ![]() и использовать его при расчете тензора поляризуемости конкретных частиц, используя формулы (6) и (7).
и использовать его при расчете тензора поляризуемости конкретных частиц, используя формулы (6) и (7).
Нами были экспериментально определены зависимости ![]() и
и ![]() при углах рассеяния
при углах рассеяния ![]() ,
, ![]() и
и ![]() . Также экспериментально определены зависимости
. Также экспериментально определены зависимости ![]() и
и ![]() . Все эти зависимости представлены на Рис. 3.
. Все эти зависимости представлены на Рис. 3.
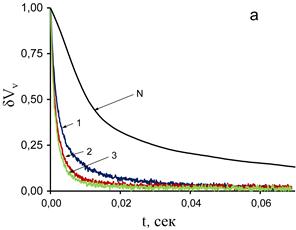
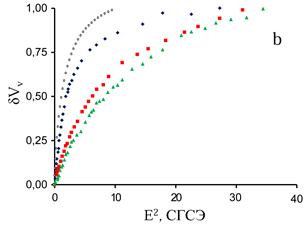
Рисунок 3. Релаксация из состояния насышенной ориентации (а) при углах рассеяния 450 (1), 900 (2), 1350 (3), дихроизм (N ) и зависимость стационарного электрооптического эффекта от поля (b) при углах рассеяния 450 (♦), 900 (■), 1350 (▲), дихроизм (○) для водной взвеси алмаза
По релаксационным зависимостям, изображенным на Рис. 3а рассчитаны функции распределения ![]() и
и ![]() , как методом нулевой регуляризации Лаврентьева [3], так и методом штрафных функций [5]. Эти функции представлены на Рис. 4а. Эти же методы были использованы для определения функций распределения
, как методом нулевой регуляризации Лаврентьева [3], так и методом штрафных функций [5]. Эти функции представлены на Рис. 4а. Эти же методы были использованы для определения функций распределения ![]() и
и ![]() при решении интегральных уравнений (9) и (10). Рассчитанные функции
при решении интегральных уравнений (9) и (10). Рассчитанные функции ![]() и
и ![]() представлены на Рис. 4b.
представлены на Рис. 4b.


Рисунок 4. Функции распределения частиц алмаза по размерам и анизотропии поляризуемости, полученные при углах рассеяния 450 (1), 900 (2), 1350 (3), дихроизм (N )
Функции ![]() и зависимости
и зависимости ![]() определенные при трех углах рассеяния использованы для расчета константы
определенные при трех углах рассеяния использованы для расчета константы ![]() , Функции
, Функции ![]() использованы для определения средних значений анизотропии поляризуемости
использованы для определения средних значений анизотропии поляризуемости ![]() частиц , вносящих вклад в величину
частиц , вносящих вклад в величину ![]() при заданном угле рассеяния. Функции
при заданном угле рассеяния. Функции ![]() использованы для определения средних значений объема
использованы для определения средних значений объема ![]() и наиболее вероятного радиуса
и наиболее вероятного радиуса ![]() частиц, вносящих вклад в величину
частиц, вносящих вклад в величину ![]() при заданном угле рассеяния. Значения
при заданном угле рассеяния. Значения ![]() ,
, ![]() ,
, ![]() и
и ![]() представлены в таблице 1 для трех углов рассеяния. Значения
представлены в таблице 1 для трех углов рассеяния. Значения![]() должны быть одинаковы для всех углов рассеяния, так как определяются только электрическими свойствами поверхности частиц и дисперсионной среды. Наблюдаемый в таблице разброс
должны быть одинаковы для всех углов рассеяния, так как определяются только электрическими свойствами поверхности частиц и дисперсионной среды. Наблюдаемый в таблице разброс ![]() может определяться неточностью функций распределения.
может определяться неточностью функций распределения.
Таблица 1.
Расчетов для частиц алмаза при![]()
|
Угол рассеяния |
|
|
|
|
|
|
1,9 |
0,76 |
1,53 |
0,22 |
|
|
0,71 |
0,70 |
0,82 |
0,19 |
|
|
0,70 |
0,61 |
0,54 |
0,18 |
Среднее значение ![]() см было использовано для расчета зависимости
см было использовано для расчета зависимости ![]() . Результаты расчета хорошо согласуются с экспериментально определенной зависимостью
. Результаты расчета хорошо согласуются с экспериментально определенной зависимостью ![]() .
.
Выводы
Проведенные исследования показывают, что геометрические и электрические характеристики частиц дисперсной фазы алмаза могут быть надежно определены при использовании недорогой аппаратуры по рассеянию света, если в исследованиях использовать электрическое поле и определять изменения характеристик рассеянного и прошедшего света взвесями частиц.
Такие исследования позволяют определять не только средние значения параметров частиц в исследуемом образце, но и распределения частиц по их геометрическим и электрическим параметрам.
Список литературы:
1.Еремова Ю.Я., Шилов В.Н. Продольная поляризация непроводящих частиц в однородном постоянном электрическом поле. Колл. Жур. — т. 37, — № 4, — 1975. — с. 635—639.
2.Еремова Ю.Я., Шилов В.Н. Поперечная поляризация непроводящих частиц в однородном постоянном электрическом поле. Колл. Жур. — т. 37, — № 6, — 1975. — с. 1090—1095.
3.Сизиков В.С. Математические методы обработки результатов измерений. СПб: Политехника, 2001. — 240 с.
4.Эскин В.Е. Рассеяние света растворами полимеров. М.: "Наука", 1973, — 352 c.
5.Babadzanjanz L., Voitylov A. Numerical methods for inverse problems in electrooptics of polydisperse colloids. Colloids and Surfaces B: Biointerfaces. Vol. 56, — Issues 1–2, — 2007. — pp. 121—125.
6.Berne B.J., Pecora R. Dynamic light scattering: with applications to Chemistry, Biology and Physics. Dover Publications Inc., 2000, — 376 p.
7.Perrin F. Mouvement brownien d'un ellipsoide I. Dispersion dielectrique pour des molecules ellipsoidales. J. Phys. Radium. — v. 5, — 1934. — p. 497—511.
8.Spartakov A.A., Trusov A.V., Voitylov A.V., Vojtylov V.V. Chap.7. P. 193—227. in Molecular and Colloid Electro-Optics, ed. By Stoylov S. and Stoimenova M., 2006. London, N.Y.: CRC Press. — 594 p.
9.Trusov A.A., Vojtylov V.V. Electrooptics and conductometry of polydisperse systems. CRC Press, Boca Raton, London, Tokyo, 1993. — 145 p.
дипломов


Оставить комментарий